
【题目】如图,抛物线y=x2﹣3x+ ![]() 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E 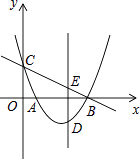
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
【答案】
(1)解:∵抛物线y=x2﹣3x+ ![]() 与x轴相交于A、B两点,与y轴相交于点C,
与x轴相交于A、B两点,与y轴相交于点C,
∴令y=0,可得x= ![]() 或x=
或x= ![]() ,
,
∴A( ![]() ,0),B(
,0),B( ![]() ,0);
,0);
令x=0,则y= ![]() ,
,
∴C点坐标为(0, ![]() ),
),
设直线BC的解析式为:y=kx+b,则有,
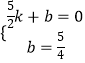 ,
,
解得: 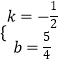 ,
,
∴直线BC的解析式为:y=- ![]() x+
x+ ![]() ;
;
(2)解:设点D的横坐标为m,则坐标为(m, ![]() ),
),
∴E点的坐标为(m, ![]() m+
m+ ![]() ),
),
设DE的长度为d,
∵点D是直线BC下方抛物线上一点,
则d= ![]() m+
m+ ![]() ﹣(m2﹣3m+
﹣(m2﹣3m+ ![]() ),
),
整理得,d=﹣m2+ ![]() m,
m,
∵a=1>0,
∴当m=﹣ ![]() =
= ![]() 时,d最大=
时,d最大= ![]() =
= ![]() =
= ![]() ,
,
∴D点的坐标为( ![]() ,
, ![]() ).
).
【解析】(1)利用坐标轴上点的特点求出A、B、C点的坐标,再用待定系数法求得直线BC的解析式;(2)设点D的横坐标为m,则纵坐标为(m, ![]() ),E点的坐标为(m,
),E点的坐标为(m, ![]() ),可得两点间的距离为d=
),可得两点间的距离为d= ![]() ,利用二次函数的最值可得m,可得点D的坐标.
,利用二次函数的最值可得m,可得点D的坐标.


科目:初中数学 来源: 题型:
【题目】若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )
A. 平均数为10,方差为2 B. 平均数为11,方差为3
C. 平均数为11,方差为2 D. 平均数为12,方差为4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,AD是
中,AD是![]() 的平分线,
的平分线,![]() ,垂足为E,作
,垂足为E,作![]() ,交直线AE于点
,交直线AE于点![]() 设
设![]() ,
,![]() .
.

![]() 若
若![]() ,
,![]() ,依题意补全图1,并直接写出
,依题意补全图1,并直接写出![]() 的度数;
的度数;
![]() 如图2,若
如图2,若![]() 是钝角,求
是钝角,求![]() 的度数
的度数![]() 用含
用含![]() ,
,![]() 的式子表示
的式子表示![]() ;
;
![]() 如图3,若
如图3,若![]() ,直接写出
,直接写出![]() 的度数
的度数![]() 用含
用含![]() ,
,![]() 的式子表示
的式子表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2﹣4ac<0;其中正确的结论有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
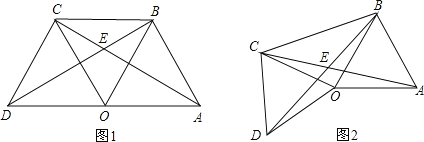
【题目】(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.

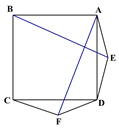

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小明和小智一起玩卡片游戏,他们分别握有三张正面分别标有字母A,B,C,的不透明卡片.游戏约定:每人将各自的卡片背面朝工弄洗均匀,然后随机抽取一张,两张卡片中,如果同为元音或辅音字母,则为平局;如果一个元音字母一个辅音字母,则抽到元音字母者获胜.
(1)请用列表或画树状图的方法列举出所有出现结果的可能性;
(2)求小明获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAD和∠CBD的平分线相交于点P.设∠CAD、∠CBD、∠C、∠D的度数依次为a、b、c、d,用仅含其中2个字母的代数式来表示∠P的度数:_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com