
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���Ӧ��C��D������AC��BD��
��1�������C��D�����ꣻ
��2����y����һ��P��0��m����mΪ������ʹ����x��y�Ķ�Ԫһ�η�����![]() ���������⣬���P�����ꣻ
���������⣬���P�����ꣻ
��3���ڣ�2���������£���Q�����߶�CD�ϣ�������Ϊn����PBQ�����S��PBQ��ֵ��С��0.6�Ҳ�����4����n��ȡֵ��Χ��

���𰸡���1��C��0��2����D��4��2������2��P��0����4������3��2.5��n��4��
��������
��1������ƽ�ƹ��ɣ�ֱ�ӵó���C��D�����ꣻ
��2�����x��![]() .�ɵ�m��ȡֵΪ��4����P������������
.�ɵ�m��ȡֵΪ��4����P������������
��3������P��x���ƽ���ߣ�����B��y���ƽ���߽�CD�ڵ�F����ƽ��ֱ�߽��ڵ�E�����S�ı���PEFC��3��6��18.����n��ʾ����PBQ��������ⲻ��ʽ��ɵó���.
�⣺��1���ߵ�A��B������ֱ�Ϊ����1��0������3��0��������A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ�õ���Ӧ��C��D��
��C��0��2����D��4��2����
��2�� ��
��
���+�ڵã�
x��![]() .
.
��x��������
��m����3.
��m����4ʱ�������������������![]() ��
��
��P��0����4����
��3������P��x���ƽ���ߣ�����B��y���ƽ���߽�CD�ڵ�F����ƽ��ֱ�߽��ڵ�E��

��S�ı���PEFC��3��6��18.
S�ı���PEFC��![]() +
+![]() ��3��4+
��3��4+![]() ��2��(3��n).
��2��(3��n).
��3n+S��PBQ+6+3��n��18.
��S��PBQ��9��2n.
��S��PBQ��ֵ��С��0.6�Ҳ�����4��
��0.6��9��2n��4.
���2.5��n��4.2.
�֡�Q�����߶�CD�ϣ�
��0��n��4��
��n��ȡֵ��Χ��2.5��n��4.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y=kx+b��ͼ���������� ![]() ͼ���ڵ�A��B����x���ڵ�C��
ͼ���ڵ�A��B����x���ڵ�C��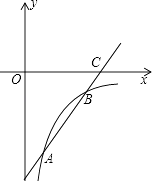
��1����m��ȡֵ��Χ��
��2������A�������ǣ�1����4������ ![]() ����m��ֵ��һ�κ����Ľ���ʽ��
����m��ֵ��һ�κ����Ľ���ʽ��
��3���ڣ�2��������£���ֱ��д������ʽ ![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ĸ���ȫ��ͬ��С���Ϸֱ�д��1��2��3��4�ĸ����֣�Ȼ��װ��һ�������Ŀڴ��ڽ��ȣ��ӿڴ���ȡ��һ����������ֺ���Ϊ��P�ĺ�����x���Żش��н��ȣ�Ȼ���ٴӴ���ȡ��һ����������ֺ���Ϊ��P��������y�����P��x��y������ֱ��y=��x+5�ϵĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֱ��������ABC�Ƶ�A��ʱ����ת15����õ���AB��C������AC=1����ͼ����Ӱ���ֵ����Ϊ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸���������̫��ˮ�ʣ����������������۹�˾��������10 ̨��ˮ�����豸������A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±�:

������:����-̨A���豸�ȹ���һ-̨B���豸��2��Ԫ������2̨A���豸�ȹ���4̨B���豸��4��Ԫ.
(1)��a��b��ֵ;
(2)��Ԥ��:�����۹�˾������ˮ�����豸���ʽ���47��Ԫ�����Ҹ���Ҫ������̫������ˮ��������1860 �֣������ļ��ֹ���?��ָ����ʡǮ��һ�ֹ�������ָ����Ӧ�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��BC��BE��AC�ڵ�E��AD��BC�ڵ�D����BAD��45�㣬AD��BE���ڵ�F��
��1����֤����ADC�ա�BDF��
��2����֤��BF��2AE��
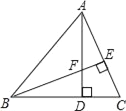
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC��![]() ����һֱ�����ǰ�
����һֱ�����ǰ�![]() ��ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
��ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
![]() ��ͼ1�е����ǰ��Ƶ�O��ÿ��
��ͼ1�е����ǰ��Ƶ�O��ÿ��![]() ���ٶ�����ʱ�뷽����תһ��
���ٶ�����ʱ�뷽����תһ��![]() ��ͼ2������t���ON����OC���ϣ���
��ͼ2������t���ON����OC���ϣ���![]() ______��
______��![]() ֱ��д���
ֱ��д���![]() ��
��
![]() ��ͼ2�����ǰ�����Ƶ�O��ÿ��
��ͼ2�����ǰ�����Ƶ�O��ÿ��![]() ���ٶ�����ʱ�뷽����ת�����OA��
���ٶ�����ʱ�뷽����ת�����OA��![]() ͬʱ����OCҲ��O����ÿ��
ͬʱ����OCҲ��O����ÿ��![]() ���ٶ�����ʱ�뷽����תһ�ܣ�
���ٶ�����ʱ�뷽����תһ�ܣ�
![]() ��OCת��9��ʱ����
��OCת��9��ʱ����![]() �Ķ�����
�Ķ�����
![]() �˶�������ʱ��
�˶�������ʱ��![]() ����˵�����ɣ�
����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ϣ�ijѧϰС�����һ�ڽ�Ϊ120���ƽ���ı���ABCD����BAD=120�㣩����̽������һ�麬60���ֱ�����ǰ���ͼ������ƽ���ı���ABCD����ƽ������ת����60��ǵĶ���ʼ�����C�غϣ��϶̵�ֱ�DZߺ�б�����ڵ���ֱ�߷ֱ��߶�AB��AD�ڵ�E��F���������߶εĶ˵㣩��
��1����������
��ͼ1����AD=AB����֤���١�BCE�ա�ACF����AE+AF=AC��
��2����ȷ���
��ͼ2����AD=2AB������C��CH��AD�ڵ�H����֤��AE=2FH��
��3������̽��
��ͼ3����AD=3AB��̽���ã� ![]() ��ֵΪ����t����t= ��
��ֵΪ����t����t= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���ͼ����A1B1C1����ABC����ƽ���ĸ���λ���Ⱥ�õ��ģ����������������ֱ�ΪA1��1��1����B1��4��2����C1��3��4����

��1���뻭����ABC����д����A��B��C�����ꣻ
��2�������AOA1�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com