
【题目】如图1,O为直线AB上一点,过点O作射线OC,![]() ,将一直角三角板
,将一直角三角板![]() 的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
![]() 将图1中的三角板绕点O以每秒
将图1中的三角板绕点O以每秒![]() 的速度沿逆时针方向旋转一周
的速度沿逆时针方向旋转一周![]() 如图2,经过t秒后,ON落在OC边上,则
如图2,经过t秒后,ON落在OC边上,则![]() ______秒
______秒![]() 直接写结果
直接写结果![]() .
.
![]() 如图2,三角板继续绕点O以每秒
如图2,三角板继续绕点O以每秒![]() 的速度沿逆时针方向旋转到起点OA上
的速度沿逆时针方向旋转到起点OA上![]() 同时射线OC也绕O点以每秒
同时射线OC也绕O点以每秒![]() 的速度沿逆时针方向旋转一周,
的速度沿逆时针方向旋转一周,
![]() 当OC转动9秒时,求
当OC转动9秒时,求![]() 的度数.
的度数.
![]() 运动多少秒时,
运动多少秒时,![]() ?请说明理由.
?请说明理由.

【答案】(1)6;(2)①![]() ②11秒或25秒,理由见解析.
②11秒或25秒,理由见解析.
【解析】
(1)因为∠AOC=30°,所以ON落在OC边上时,三角板旋转了30°,即可求出旋转时间;
(2)在整个旋转过程中,可以看做这样一个追及问题更容易理解,即:ON绕点O以每秒5°的速度沿逆时针方向旋转,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转;
①9秒时,∠NOC=45°,而OC旋转了90°,所以∠MOC的度数就是45°;
②∠MOC=35°时,应分OC与OM重合前35°与重合后35°两种情况考虑,分别进行求解即可.
![]() ,
,
而三角板每秒旋转![]() ,
,
![]() 当ON落在OC边上时,有
当ON落在OC边上时,有![]() ,
,
得![]() ,
,
故答案为6;
![]() 当OC转动9秒时,
当OC转动9秒时,![]() ,
,
而![]() ,
,
又![]() ,
,
即:![]() ,
,
答:当OC转动9秒时,![]() 的度数为
的度数为![]() ;
;
![]() 设OC运动起始位置为射线
设OC运动起始位置为射线![]() 如图
如图![]() ,运动t秒时,
,运动t秒时,![]() ,
,

则![]() ,
,![]() ,
,
当![]() 时,有
时,有![]() 或
或![]() ,
,
得![]() 或
或![]() ,
,
因为三角板与射线OC都只旋转一周,所以不考虑再次追及的情况,
故当运动11秒或25秒时,![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,完成下列问题:
,完成下列问题:
(1)求此函数图像与x轴、y轴的交点坐标;
(2)画出此函数的图像;观察图像,当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(3)平移一次函数![]() 的图像后经过点(-3,1),求平移后的函数表达式.
的图像后经过点(-3,1),求平移后的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
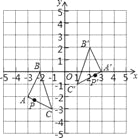
A. (﹣a,b﹣2) B. (﹣a,b+2) C. (﹣a+2,﹣b) D. (﹣a+2,b+2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C,D,连接AC,BD.
(1)求出点C,D的坐标;
(2)设y轴上一点P(0,m),m为整数,使关于x,y的二元一次方程组![]() 有正整数解,求点P的坐标;
有正整数解,求点P的坐标;
(3)在(2)的条件下,若Q点在线段CD上,横坐标为n,△PBQ的面积S△PBQ的值不小于0.6且不大于4,求n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1: ![]() 的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)
的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)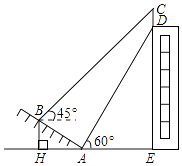
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年北京奥运会后,同学们参与体育锻炼的热情高涨.为了解他们平均每周的锻炼时间,小明同学在校内随机调查了50名同学,统计并制作了如下的频数分布表和扇形统计图.根据上述信息解答下列问题: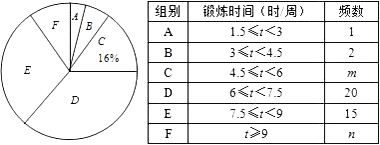
(1)m= , n=;
(2)在扇形统计图中,D组所占圆心角的度数为度;
(3)全校共有3000名学生,估计该校平均每周体育锻炼时间不少于6小时的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何证明:
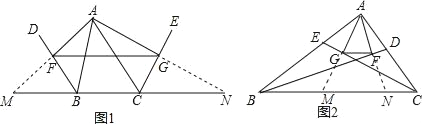
(1)已知:如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG,延长AF、AG,与直线BC相交.求证:FG=![]() (AB+BC+AC).
(AB+BC+AC).
(2)若BD、CE分别是△ABC的内角平分线,其余条件不变(如图1),线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com