
����Ŀ��Ϊ�˸���������̫��ˮ�ʣ����������������۹�˾��������10 ̨��ˮ�����豸������A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±�:

������:����-̨A���豸�ȹ���һ-̨B���豸��2��Ԫ������2̨A���豸�ȹ���4̨B���豸��4��Ԫ.
(1)��a��b��ֵ;
(2)��Ԥ��:�����۹�˾������ˮ�����豸���ʽ���47��Ԫ�����Ҹ���Ҫ������̫������ˮ��������1860 �֣������ļ��ֹ���?��ָ����ʡǮ��һ�ֹ�������ָ����Ӧ�ķ���.
���𰸡�(1) ![]() �� (2) ����:��A���豸1̨��B���豸9̨:��A���豸2̨��B���豸8̨;
�� (2) ����:��A���豸1̨��B���豸9̨:��A���豸2̨��B���豸8̨;
��A���豸3̨��B���豸7̨����ʡǮ�Ĺ�����ѡ��A���豸1̨��B���豸9̨������42��.
��������
(1) ����A�͵ļ۸���a��Ԫ������B�͵��豸b��Ԫ�����ݹ���һ-̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���4̨B���豸��4��Ԫ���з�������⣻
(2)�蹺��A�ͺ��豸x̨����B��Ϊ(0-x)̨������ʹ���۹�˾������ˮ�����豸���ʽ���47��Ԫ������ÿ��Ҫ������ˮ��������1860 �֣����в���ʽ�����.
(1) ��������ã�![]() ��
��
���: ![]() ��
��
(2)�蹺����ˮ�����豸A���豸x̨��B���豸![]() ̨��
̨��
��������ã�![]() ��
��
��ã�![]() ��
��
��xΪ1��2��3.
����:��A���豸1̨��B���豸9̨��
��A���豸2̨��B���豸8̨��
��A���豸3̨��B���豸7̨��
��Ϊ�˽�Լ�ʽ�Ӧѡ��A���豸1̨��B���豸9̨�������=![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
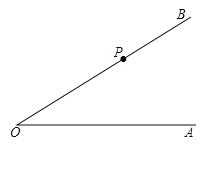
����Ŀ����������Ҫ��ͼ����գ�
��ͼ����![]() ��
��![]() �ı�
�ı�![]() �ϵ�һ�㣬
�ϵ�һ�㣬
��1������![]() ��
��![]() �Ĵ��ߣ���
�Ĵ��ߣ���![]() �ڵ�
�ڵ�![]() ��
��
��2���ڣ�1���Ļ�������![]() �ı�
�ı�![]() �ϵĸߣ�����Ϊ
�ϵĸߣ�����Ϊ![]() ��
��
��3���߶�___________�ij����ǵ�![]() ��ֱ��
��ֱ��![]() �ľ��룻
�ľ��룻
��4���߶�![]() �������߶δ�С��ϵ��___________������<�������ӣ���
�������߶δ�С��ϵ��___________������<�������ӣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ԲO��Rt��ABC�����Բ����ACB=90�㣬��A=25�㣬����C��ԲO�����ߣ���AB���ӳ����ڵ�D�����D�Ķ����ǣ� �� 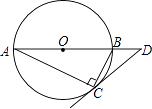
A.25��
B.40��
C.50��
D.65��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ѡ�ABC����һ���ı任�õ���A��B��C�䣬�����ABC���ϵ�P������Ϊ��a��b������ô������ڡ�A��B��C���еĶ�Ӧ��P�������Ϊ��������
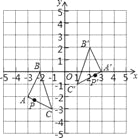
A. ����a��b��2�� B. ����a��b+2�� C. ����a+2����b�� D. ����a+2��b+2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=3��B��AB=10��AC=4��ADƽ����BAC����BC�ڵ�D��CE��AD��E����CE= ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���Ӧ��C��D������AC��BD��
��1�������C��D�����ꣻ
��2����y����һ��P��0��m����mΪ������ʹ����x��y�Ķ�Ԫһ�η�����![]() ���������⣬���P�����ꣻ
���������⣬���P�����ꣻ
��3���ڣ�2���������£���Q�����߶�CD�ϣ�������Ϊn����PBQ�����S��PBQ��ֵ��С��0.6�Ҳ�����4����n��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��¥�Ķ�������һ������CD��С����ɽ�µ��½�A����ù���Ƶ�����Ϊ60�㣬���¶�Ϊ1�� ![]() ������AB�������ߵ�B������ù���ƶ���C������Ϊ45�㣬��֪AB=10m��AE=15m��������CD�ĸ߶ȣ���ȷ��0.1m������ǵĸ߶Ⱥ��Բ��ƣ�
������AB�������ߵ�B������ù���ƶ���C������Ϊ45�㣬��֪AB=10m��AE=15m��������CD�ĸ߶ȣ���ȷ��0.1m������ǵĸ߶Ⱥ��Բ��ƣ�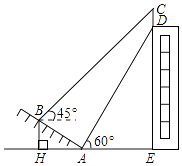
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֤��:
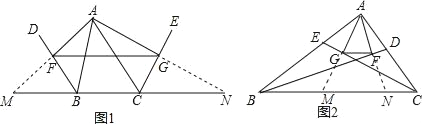
��1����֪����ͼ1��BD��CE�ֱ��ǡ�ABC�����ƽ���ߣ�����A��AF��BD��AG��CE������ֱ���F��G������FG���ӳ�AF��AG����ֱ��BC�ཻ����֤��FG��![]() ��AB+BC+AC����
��AB+BC+AC����
��2����BD��CE�ֱ��ǡ�ABC���ڽ�ƽ���ߣ������������䣨��ͼ1�����߶�FG���ABC����������������������ϵ��д����IJ��룬������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A�������϶�Ӧ����Ϊa����B�������϶�Ӧ����Ϊb����|a+3|+|b-2|=0��A,B ֮��ľ����Ϊ|AB|.��ش����⣺
(1)ֱ��д��a,b, |AB|��ֵ. a= ��b = �� |AB|= ��
(2)���P�������϶�Ӧ����Ϊx����|PA|-|PB|=2ʱ����x��ֵ��
(3)����P�ڵ�A����࣬M��N�ֱ���PA��PB���е�.����P�ڵ�A������ƶ�ʱ��ʽ��|PN|-|PM|��ֵ�Ƿ����ı䣿�����䣬�������ֵ���������仯����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com