
| A.第8秒 | B.第10秒 | C.第12秒 | D.第15秒 |
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源:不详 题型:解答题
 的图像过点
的图像过点 ,与
,与 轴交于点
轴交于点 .
.
 (其中
(其中 是原点);
是原点); ,使
,使 的值最小;
的值最小; 是线段
是线段 上的一个动点(不与
上的一个动点(不与 、
、 重合),过
重合),过 作
作 轴的平行线,分别交此二次函数图像及
轴的平行线,分别交此二次函数图像及 轴于
轴于 、
、 两点 . 请问
两点 . 请问 ,使
,使 . 若存在,
. 若存在, 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.0<t<2 | B.0<t<1 | C.1<t<2 | D.﹣1<t<1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 过点P作
过点P作 x轴交(1)中的抛物线于点Q,当以
x轴交(1)中的抛物线于点Q,当以 为顶点的三角形与
为顶点的三角形与 相似时,求点P的坐标.
相似时,求点P的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
| x | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | -14 | -7 | -2 | 2 | m | n | -7 | -14 | -23 |
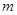 = ,
= ,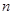 = .
= .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 轴上,折叠边AD,使点D落在
轴上,折叠边AD,使点D落在 轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为
轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为 ,其中
,其中 >0.
>0.
 的式子表示);
的式子表示);  的值;
的值;  经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求
经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求 、
、 、
、 的值.
的值. 查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ]为函数
]为函数 的特征数, 下面给出特征数为 [2m,1 – m , –1– m] 的函数的一些结论: ( )
的特征数, 下面给出特征数为 [2m,1 – m , –1– m] 的函数的一些结论: ( )  ,
, );
);  ;
;  时,y随x的增大而减小;
时,y随x的增大而减小;| A.①④ | B.①③④ | C. ①②④ | D.①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com