
 如图,双曲线y=$\frac{2}{x}$(x>0),y=$\frac{12}{x}$(x>0),P、Q为y轴正半轴上两点,设P点的坐标为(0,a-2),PQ=4,分别过P、Q两点作x轴的平行线交两支曲线于C、D、A、B(如图)
如图,双曲线y=$\frac{2}{x}$(x>0),y=$\frac{12}{x}$(x>0),P、Q为y轴正半轴上两点,设P点的坐标为(0,a-2),PQ=4,分别过P、Q两点作x轴的平行线交两支曲线于C、D、A、B(如图)分析 (1)用a的代数式表示A、B、C、D的坐标,根据CD=3AB,列出方程即可解决问题;
(2)首先证明∠APQ=∠PDQ,由tan∠APQ=tan∠PDQ,可得$\frac{AQ}{PQ}$=$\frac{PQ}{PD}$,由此列出方程即可解决问题;
(3)①当四边形PQBC为矩形时,根据QB=PC,列出方程即可解决问题;
②用k的代数式表示Ck-3、Bk-3的坐标,根据题意列出不等式组即可解决问题;
解答 解:(1)由题意Q(0,a+2),A($\frac{2}{a+2}$,a+2),B($\frac{12}{a+2}$,a+2),C($\frac{2}{a-2}$,a-2),D($\frac{12}{a-2}$,a-2),
∵CD=3AB,
∴$\frac{12}{a-2}$-$\frac{2}{a-2}$=3($\frac{12}{a+2}$-$\frac{2}{a+2}$),
解得a=4.
经检验a=4是分式方程的解.
∴a=4.
(2)如图连接PA、DQ交于点G.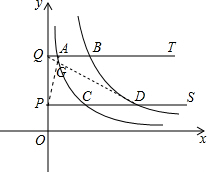
∵PA⊥DQ,
∴∠PGD=90°,
∴∠APQ+∠DPG=90°,∠DPG+∠PDG=90°,
∴∠APQ=∠PDQ,
∴tan∠APQ=tan∠PDQ,
∴$\frac{AQ}{PQ}$=$\frac{PQ}{PD}$,
∴$\frac{\frac{2}{a+2}}{4}$=$\frac{4}{\frac{12}{a-2}}$.
解得a=$\frac{\sqrt{22}}{2}$或-$\frac{\sqrt{22}}{2}$(舍弃),
经检验a=$\frac{\sqrt{22}}{2}$是分式方程的解,且符合题意.
(3)①当四边形PQBC是矩形时,QB=PC,
∴$\frac{12}{a+2}$=$\frac{2}{a-2}$,
解得a=$\frac{14}{5}$,
经检验a=$\frac{14}{5}$的分式方程的解,且符合题意.
②由①可知P(0,$\frac{4}{5}$),C($\frac{5}{2}$,$\frac{4}{5}$),
∵C1C=C2C1=…=CkCk-1=PC,
∴Ck-3([(k-2)$\frac{5}{2}$,$\frac{4}{5}$],Bk-3[(k-2)$\frac{5}{2}$,$\frac{24}{5}$],
由题意$\frac{4}{5}$≤$\frac{k}{(k-2)\frac{5}{2}}$≤$\frac{24}{5}$,
解得$\frac{24}{11}$≤k≤4,
∵K是整数,
∴k=4或3(舍弃),
∴k=4.
点评 本题考查反比例函数综合题、矩形的判定和性质、分式方程的解,不等式等知识,解题的关键是学会利用参数解决问题,学会构建方程或不等式解决实际问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
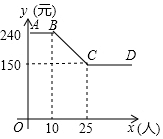 某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
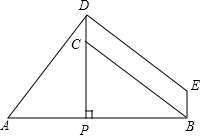 如图,点P在线段AB上,PD⊥AB,点C在线段PD上,连结BC,以CB,CD为邻边构造□BCDE,若AD=DE,AP=PC.
如图,点P在线段AB上,PD⊥AB,点C在线段PD上,连结BC,以CB,CD为邻边构造□BCDE,若AD=DE,AP=PC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com