
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本![]() (单位:元)、销售价
(单位:元)、销售价![]() (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?

【答案】(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)y=﹣0.2x+60(0≤x≤90);(3)当该产品产量为75kg时,获得的利润最大,最大值为2250.
【解析】
试题分析:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可;
(3)利用总利润=单位利润×产量列出有关x的二次函数,求得最值即可.
试题解析:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)设线段AB所表示的![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,∵
,∵![]() 的图象过点(0,60)与(90,42),∴
的图象过点(0,60)与(90,42),∴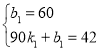 ,∴解得:
,∴解得: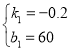 ,
,
∴这个一次函数的表达式为:y=﹣0.2x+60(0≤x≤90);
(3)设![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,
,
∵经过点(0,120)与(130,42),∴![]() ,解得:
,解得:![]() ,
,
∴这个一次函数的表达式为![]() (0≤x≤130),
(0≤x≤130),
设产量为xkg时,获得的利润为W元,
当0≤x≤90时,W=![]() =
=![]() ,
,
∴当x=75时,W的值最大,最大值为2250;
当90≤x130时,W=![]() =
=![]() ,
,
∴当x=90时,W=![]() ,
,
由﹣0.6<0知,当x>65时,W随x的增大而减小,∴90≤x≤130时,W≤2160,
因此当该产品产量为75kg时,获得的利润最大,最大值为2250.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】某兴趣小组决定去市场购买A,B,C三种仪器,其单价分别为3元,5元,7元,购买这批仪器需花62元;经过讨价还价,最后以每种单价各下降1元成交,结果只花50元就买下了这批仪器.那么A种仪器最多可买( )
A.8件 B.7件 C.6件 D.5件
查看答案和解析>>
科目:初中数学 来源: 题型:
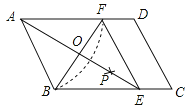
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是 ;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 ,∠ABC= °.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.概率很小的事件不可能发生
B.随机事件发生的概率为1
C.不可能事件发生的概率为0
D.投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次
查看答案和解析>>
科目:初中数学 来源: 题型:
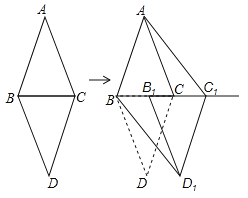
【题目】如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市将大、中、小学生的视力进行抽样分析,其中大、中、小学生的人数比为2:3:5,若已知中学生被抽到的人数为150人,则应抽取的样本容量等于( )
(A)1500 (B)1000 (C)150 (D)500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.(不写解答过程,直接写出结果)
(1)若△A1B1C1与△ABC关于原点O成中心对称,则点A1的坐标为 ;
(2)将△ABC向右平移4个单位长度得到△A2B2C2,则点B2的坐标为 ;
(3)将△ABC绕O点顺时针方向旋转90°,则点C走过的路径长为 ;
(4)在x轴上找一点P,使PA+PB的值最小,则点P的坐标为 .
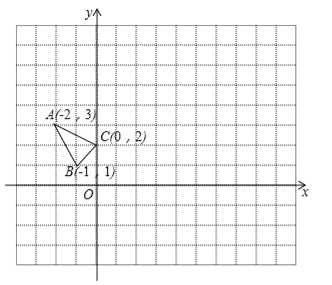
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个图形绕着某一点旋转________,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或________,这个点叫做它们的________.这两个图形在旋转后能重合的对应点叫做关于对称中心的________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (k>0).
(k>0).
(1)当k=![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证:![]() .
.
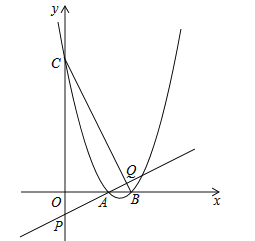
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com