
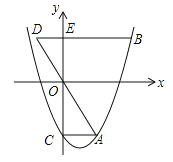
����Ŀ����ABC��ƽ��ֱ������ϵxOy�е�λ����ͼ��ʾ������д�����̣�ֱ��д�������
��1������A1B1C1���ABC����ԭ��O�����ĶԳƣ����A1������Ϊ ��
��2������ABC����ƽ��4����λ���ȵõ���A2B2C2�����B2������Ϊ ��
��3������ABC��O��˳ʱ�뷽����ת90�㣬���C�߹���·����Ϊ ��
��4����x������һ��P��ʹPA+PB��ֵ��С�����P������Ϊ ��
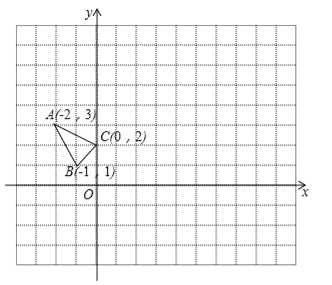
���𰸡���1����2����3������2����3��1������3��������4����![]() ��0����
��0����
��������
�����������1�����ù���ԭ�����ĶԳƵĵ������������⣻
��2�����õ��ƽ�ƹ�����⣻
��3����C�߹���·��Ϊ�Ե�OΪԲ�ģ�OCΪ�뾶��Բ�Ľ�Ϊ90�ȵĻ���Ȼ����ݻ�����ʽ�����C�߹���·������
��4����ȷ����B����x��ĶԳƵ�B������Ϊ����1����1��������AB�佻x����P�㣬��������֮���߶���̿�ȷ��PA+PB��ֵ��С���������ô���ϵ�������ֱ��AB��Ľ���ʽ��Ȼ����ֱ��AB����x��Ľ�������Ϳ��õ���P�����꣮
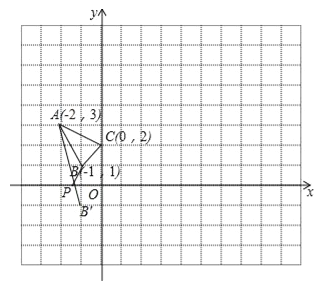
�����������1������A1B1C1���ABC����ԭ��O�����ĶԳƣ����A1������Ϊ��2����3����
��2������ABC����ƽ��4����λ���ȵõ���A2B2C2�����B2������Ϊ��3��1����
��3������ABC��O��˳ʱ�뷽����ת90�㣬���C�߹���·����=![]() =�У�
=�У�
��4��B�����x��ĶԳƵ�B������Ϊ����1����1��������AB�佻x����P�㣬��PA+PB=PA+PB��=AB�䣬��ʱPA+PB��ֵ��С����ֱ��AB��Ľ���ʽΪy=kx+b����A����2��3����B�䣨��1����1���������![]() ������
������![]() ������ֱ��AB��Ľ���ʽΪy=��4x��5����y=0ʱ����4x��5=0�����x=
������ֱ��AB��Ľ���ʽΪy=��4x��5����y=0ʱ����4x��5=0�����x=![]() �����Դ�ʱ��P������Ϊ��
�����Դ�ʱ��P������Ϊ��![]() ��0����
��0����
�ʴ�Ϊ����2����3������3��1�����У���![]() ��0����
��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����λ�̳ABCD�ܳ���80m����ABC=60�㣬�������εĶԽ�����������С·AC��BD���ཻ��O�㣮 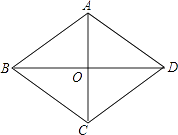
��1��������С·�ij�AC��BD����������ø��ű�ʾ��
��2����̳���������������ø��ű�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�������ȷ���ǣ�������
A.2a+3a��5aB.a3a2��a6
C.��a��b��2��a2+b2D.����a2��3����a5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ����������ij�ֲ�Ʒ�������������������ȣ���ͼ�е�����ABD���߶�CD�ֱ��ʾ�ò�Ʒÿǧ�������ɱ�![]() ����λ��Ԫ�������ۼ�
����λ��Ԫ�������ۼ�![]() ����λ��Ԫ�������x����λ��kg��֮��ĺ�����ϵ��
����λ��Ԫ�������x����λ��kg��֮��ĺ�����ϵ��
��1�������ͼ�е�D�ĺ����ꡢ�������ʵ�����壻
��2�����߶�AB����ʾ��![]() ��x֮��ĺ�������ʽ��
��x֮��ĺ�������ʽ��
��3�����ò�Ʒ����Ϊ����ʱ����õ����������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����һ�ֲ�Ʒ2013��IJ�����100������ƻ�2015������ﵽ121���������2013�굽2015�����ֲ�Ʒ����������������ͬ����2013�굽2015�����ֲ�Ʒ�������������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ε����߷ֱ�Ϊa��b��c,�ң�a-b��2+��a2+b2-c2��2=0,�������ε���״Ϊ����������������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����ͼ1����P��x��y����ƽ��ֱ�������У�����P��PA��x�ᣬ����ΪA������P�ƴ���A˳ʱ����ת�Ǧ���0�㣼����90�㣩�õ���Ӧ��P�䣬���dzƵ�P����P����˶�Ϊ��б���˶������磺��P��0��2����б30���˶���Ķ�Ӧ��ΪP�䣨1��![]() ����
����
ͼ��E��ƽ��ֱ������ϵ�У�ͼ��E�ϵ����е㶼����б���˶���õ�ͼ��E�䣬�������˶���Ϊͼ��E����б���˶���
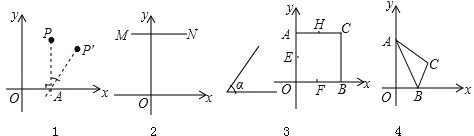
����
��1����Q��1��2����б60���˶���Ķ�Ӧ��Q�������Ϊ ��
��2����ͼ2��ƽ����x����߶�MN��б���˶���õ���Ӧ�߶�M��N�䣬M��N����MNƽ���������˵�����ɣ�
Ӧ�ã���1����ͼ3��������AOBC��б���˶���������е�E��F��G��H�Ķ�Ӧ��E�䣬F�䣬G�䣬H�乹�ɵ��ı�����ʲô�����ı��Σ� ��
��2����ͼ4����֪��A��0��4����B��2��0����C��3��2��������ABC��б���˶����ܲ��ܵõ�Rt��A��B��C�䣬�ҡ�A��C��B��Ϊֱ�ǣ����е�A�䣬B�䣬C��Ϊ��A��B��C�Ķ�Ӧ�㣮�����cos����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A��a��2��3���͵�B����1��b+5������y��Գƣ����C��a��b���ڣ� ��
A.��һ����
B.�ڶ�����
C.��������
D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��m��0����y���ڵ�C��CA��y�ᣬ���������ڵ�A����B���������ϣ����ڵ�һ�����ڣ�BE��y�ᣬ��y���ڵ�E����AO���ӳ����ڵ�D��BE=2AC��
��m��0����y���ڵ�C��CA��y�ᣬ���������ڵ�A����B���������ϣ����ڵ�һ�����ڣ�BE��y�ᣬ��y���ڵ�E����AO���ӳ����ڵ�D��BE=2AC��
��1���ú�m�Ĵ���ʽ��ʾBE�ij���
��2����m=![]() ʱ���жϵ�D�Ƿ������������ϣ���˵�����ɣ�
ʱ���жϵ�D�Ƿ������������ϣ���˵�����ɣ�
��3����AG��y�ᣬ��OB�ڵ�F����BD�ڵ�G��
������DOE���BGF�������ȣ���m��ֵ��
������AE����OB�ڵ�M������AMF���BGF�������ȣ���m��ֵ�� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com