
【题目】阅读:如图1,点P(x,y)在平面直角坐标中,过点P作PA⊥x轴,垂足为A,将点P绕垂足A顺时针旋转角α(0°<α<90°)得到对应点P′,我们称点P到点P′的运动为倾斜α运动.例如:点P(0,2)倾斜30°运动后的对应点为P′(1,![]() ).
).
图形E在平面直角坐标系中,图形E上的所有点都作倾斜α运动后得到图形E′,这样的运动称为图形E的倾斜α运动.
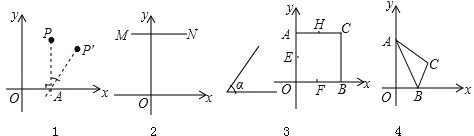
理解
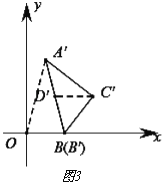
(1)点Q(1,2)倾斜60°运动后的对应点Q′的坐标为 ;
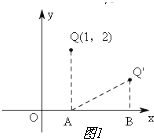
(2)如图2,平行于x轴的线段MN倾斜α运动后得到对应线段M′N′,M′N′与MN平行且相等吗?说明理由.
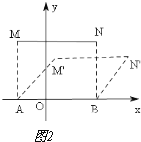
应用:(1)如图3,正方形AOBC倾斜α运动后,其各边中点E,F,G,H的对应点E′,F′,G′,H′构成的四边形是什么特殊四边形: ;
(2)如图4,已知点A(0,4),B(2,0),C(3,2),将△ABC倾斜α运动后能不能得到Rt△A′B′C′,且∠A′C′B′为直角,其中点A′,B′,C′为点A,B,C的对应点.请求出cosα的值.
【答案】理解(1)(![]() ,1);(2)M′N′与MN平行且相等;应用(1)矩形;(2)
,1);(2)M′N′与MN平行且相等;应用(1)矩形;(2)![]() .
.
【解析】
试题分析:理解:
(1)根据题目中称点P到P′的运动为倾α运动的定义来求Q′的坐标;
(2)根据题目中图形E的倾α运动的定义可以判断M′N′与MN的关系;
应用:
(1)参考理解(2)可得,正方形AOBC旋转后形成菱形,菱形的四边中点组成的四边形是矩形;
(2)先求出A′B′=4=OA′,利用三角函数求得cosα的值.
试题解析:(1)如图1,过点Q作QA⊥x轴,垂足为A,过旋转Q′作x轴的垂线,垂足为B,在Rt△ABQ′中,∠Q′AB=30°,BQ′=1,由勾股定理得AB=![]() ,∴OB=
,∴OB=![]() ,∴Q′的坐标为(
,∴Q′的坐标为(![]() ,1).故答案为:(
,1).故答案为:(![]() ,1);
,1);
(2)M′N′与MN平行且相等,理由如下:
如图2,分别过点M、N作MA⊥x轴于点A,NB⊥x轴于点B,∴MN∥AB,且MN=AB,由定义可知,M′A∥N′B,M′A=N′B,∴四边M′ABN′是平行四边形,∴M′N′∥AB,M′N′=AB,∴M′N′与MN平行且相等.
应用:(1)由理解(2)可得,正方形AOBC旋转后形成菱形,菱形的四边中点组成的四边形是矩形.
故答案为:矩形;
(2)能,cosα=![]() .如图3,设AB的中点为D,∴D点坐标为(1,2),∴CD∥x轴,且CD=2,∵D点对应点D′是A′B′中点,C′D′=2,∴C′D′=
.如图3,设AB的中点为D,∴D点坐标为(1,2),∴CD∥x轴,且CD=2,∵D点对应点D′是A′B′中点,C′D′=2,∴C′D′=![]() A′B′,∴A′B′=4=OA′,∵∠α=
A′B′,∴A′B′=4=OA′,∵∠α=![]() ∠OA′B′,∴cosα=
∠OA′B′,∴cosα=![]() .
.


科目:初中数学 来源: 题型:
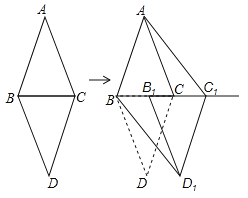
【题目】如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
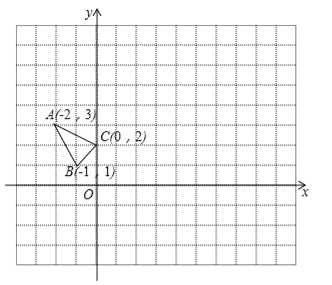
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.(不写解答过程,直接写出结果)
(1)若△A1B1C1与△ABC关于原点O成中心对称,则点A1的坐标为 ;
(2)将△ABC向右平移4个单位长度得到△A2B2C2,则点B2的坐标为 ;
(3)将△ABC绕O点顺时针方向旋转90°,则点C走过的路径长为 ;
(4)在x轴上找一点P,使PA+PB的值最小,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( ) 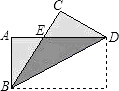
A.△EBD是等腰三角形,EB=ED
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个图形绕着某一点旋转________,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或________,这个点叫做它们的________.这两个图形在旋转后能重合的对应点叫做关于对称中心的________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查的是( )
A. 对常州市居民日平均用水量的调查
B. 对一批LED节能灯使用寿命的调查
C. 对常州新闻频道“政风热线”栏目收视率的调查
D. 对某校八年级(2)班同学的视力情况的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
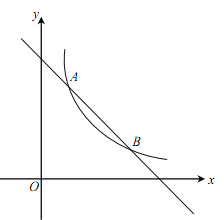
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com