
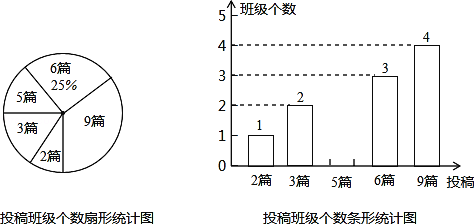
【题目】为积极响应市委,市政府提出的“实现伟大中国梦,建设美丽新城市”的号召,我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的两个班级中,八,九年级各有两个班,校学生会准备从这四个中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
【答案】(1)30°.(2)6.(3)![]() .
.
【解析】
试题分析:(1)根据投稿6篇的班级个数是3个,所占的比例是25%,可求总共班级个数,利用投稿篇数为2的比例乘以360°即可求解;
(2)根据加权平均数公式可求该校八,九年级各班在这一周内投稿的平均篇数,再用总共班级个数-不同投稿情况的班级个数即可求解:
(3)利用树状图法,然后利用概率的计算公式即可求解.
试题解析:(1)3÷25%=12(个),
![]() ×360°=30°.
×360°=30°.
故投稿篇数为2所对应的扇形的圆心角的度数为30°;
(2)12-1-2-3-4=2(个),
(2+3×2+5×2+6×3+9×4)÷12
=72÷12
=6(篇),
将该条形统计图补充完整为:
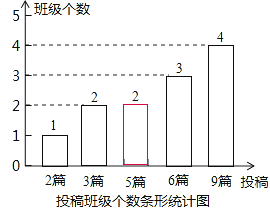
(3)画树状图如下:
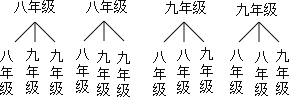
总共12种情况,不在同一年级的有8种情况,
所选两个班正好不在同一年级的概率为:8÷12=![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法:①三点确定一个圆;②垂直于弦的直径平分弦及弦所对的两条弧;③三角形的外心到三条边的距离相等;④圆的切线垂直于经过切点的半径.正确的个数是( )
A. 0 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
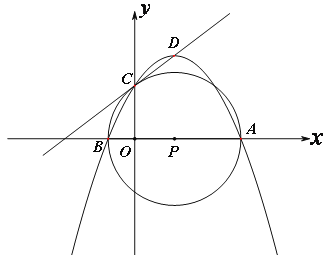
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c经过点A(4,0)、B(-1,0),与y轴交于点C,D为抛物线的顶点,过A、B、C 作⊙P.
x2+bx+c经过点A(4,0)、B(-1,0),与y轴交于点C,D为抛物线的顶点,过A、B、C 作⊙P.
(1)求b、c的值;
(2)求证:线段AB是⊙P的直径;
(3)连接AC,AD,在坐标平面内是否存在点Q,使得△CDA~△CPQ,若存在,求出点Q的坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
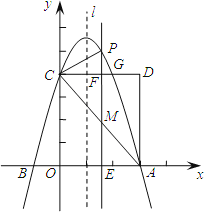
【题目】如图,抛物线![]() (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
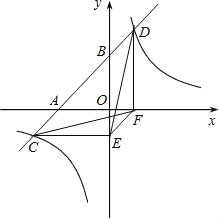
【题目】 如图,一次函数y=x+3的图象与x轴,y轴交于A,B两点,与反比例函数![]() 的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④AC=BD.
其中正确的结论是( )
A.①② B.①②③
C.①②③④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有10人,请解答下列问题:
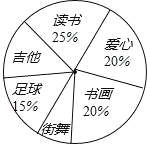
(1)该班的学生共有 名;该班参加“爱心社”的人数为 名,若该班参加“吉他社”与“街舞社”的人数相同,则“吉他社”对应扇形的圆心角的度数为 ;
(2)一班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+8x+9=0,变形后的结果正确的是( )
A. (x+4)2=﹣7 B. (x+4)2=﹣9 C. (x+4)2=7 D. (x+4)2=25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com