
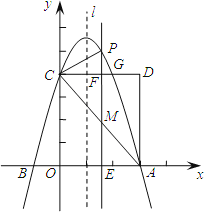
����Ŀ����ͼ��������![]() ��a��0����x����A��B���㣬A������Ϊ��3��0������y�ύ�ڵ�C��0��4������OC��OAΪ��������OADC���������ڵ�G��
��a��0����x����A��B���㣬A������Ϊ��3��0������y�ύ�ڵ�C��0��4������OC��OAΪ��������OADC���������ڵ�G��
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ���l�ڱ�OA��������O��A���㣩��ƽ���ƶ����ֱ�x���ڵ�E����CD�ڵ�F����AC�ڵ�M�����������ڵ�P������M�ĺ�����Ϊm�����ú�m�Ĵ���ʽ��ʾPM�ij���
��3���ڣ�2���������£�����PC������CD�Ϸ��������߲����Ƿ���������ĵ�P��ʹ����P��C��FΪ����������κ���AEM���ƣ������ڣ������ʱm��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=-![]() x2+
x2+![]() x+4����2��PM=-
x+4����2��PM=-![]() m2+4m��0��m��3������3�����������ĵ�Pʹ��PFC����AEM���ƣ���ʱm��ֵΪ
m2+4m��0��m��3������3�����������ĵ�Pʹ��PFC����AEM���ƣ���ʱm��ֵΪ![]() ��1��
��1��
��������
�����������1����A��3��0����C��0��4������y=ax2-2ax+c�����ô���ϵ����������������ߵĽ���ʽ��
��2���ȸ���A��C�����꣬�ô���ϵ�������ֱ��AC�Ľ���ʽ���������������ߺ�ֱ��AC�Ľ���ʽ�ֱ��ʾ����P����M�����꣬���ɵõ�PM�ij���
��3��������PFC����AEM����ֱ�ǣ�F��E��Ӧ��������P��C��FΪ����������κ���AEM����ʱ������������������ۣ��١�PFC�ס�AEM���ڡ�CFP�ס�AEM���ɷֱ��ú�m�Ĵ���ʽ��ʾ��AE��EM��CF��PF�ij����������������ζ�Ӧ�ߵı�����г�����ʽ�����m��ֵ��
�����������1����������y=ax2-2ax+c��a��0��������A��3��0������C��0��4����
��![]() ��
��
���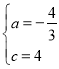 ��
��
�������ߵĽ���ʽΪy=-![]() x2+
x2+![]() x+4��
x+4��
��2����ֱ��AC�Ľ���ʽΪy=kx+b��
��A��3��0������C��0��4����
��![]() ��
��
���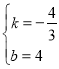 ��
��
��ֱ��AC�Ľ���ʽΪy=-![]() x+4��
x+4��
����M�ĺ�����Ϊm����M��AC�ϣ�
��M���������m��-![]() m+4����
m+4����
����P�ĺ�����Ϊm����P��������y=-![]() x2+
x2+![]() x+4�ϣ�
x+4�ϣ�
����P��������m��-![]() m2+
m2+![]() m+4����
m+4����
��PM=PE-ME=��-![]() m2+
m2+![]() m+4��-��-
m+4��-��-![]() m+4��=-
m+4��=-![]() m2+4m��
m2+4m��
��PM=-![]() m2+4m��0��m��3����
m2+4m��0��m��3����
��3���ڣ�2���������£�����PC����CD�Ϸ��������߲��ִ��������ĵ�P��ʹ����P��C��FΪ����������κ���AEM���ƣ��������£������⣬�ɵ�AE=3-m��EM=-![]() m+4��CF=m������P��C��FΪ����������κ���AEM���ƣ������
m+4��CF=m������P��C��FΪ����������κ���AEM���ƣ������
��P����CD�Ϸ�����PF=-![]() m2+
m2+![]() m+4-4=-
m+4-4=-![]() m2+
m2+![]() m��
m��
����PFC�ס�AEM����PF��AE=FC��EM��
����-![]() m2+
m2+![]() m������3-m��=m����-
m������3-m��=m����-![]() m+4����
m+4����
��m��0��m��3��
��m=![]() ��
��
������CFP�ס�AEM����CF��AE=PF��EM��
��m����3-m��=��-![]() m2+
m2+![]() m������-
m������-![]() m+4����
m+4����
��m��0��m��3��
��m=1��
�������������������ĵ�Pʹ��PFC����AEM���ƣ���ʱm��ֵΪ![]() ��1��
��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��ͼ1�������߾���A��1��0����B��7��0����D��0��![]() �� ���㣬��ABΪ����x���Ϸ����ȱ�������ABC.
�� ���㣬��ABΪ����x���Ϸ����ȱ�������ABC.
��1���������ߵĽ���ʽ��
��2����������x���Ϸ��Ƿ���ڵ�M��ʹS��ABM =![]() S��ABC�����������������M�������������ڣ���˵�����ɣ�
S��ABC�����������������M�������������ڣ���˵�����ɣ�
��3����ͼ2��E���߶�AC�ϵĶ��㣬F���߶�BC�ϵĶ��㣬AF��BE�ཻ�ڵ�P.
����CE=BF���Բ���AF��BE��������ϵ����˵�����ɣ��������APB�Ķ�����
����AF=BE������E��A�˶���Cʱ�������P������·����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ���ʽ2x2��xy3+18�У�������ߵ������� ��
A. 2 B. 18 C. 2x2 D. ��xy3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ε��ڽǺͱ���Ǻ͵�������180���������������ǣ� ��
A. ����� B. ������ C. �߱��� D. �˱���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
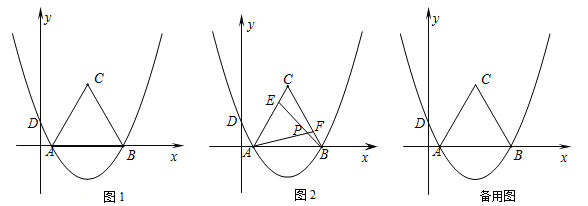
����Ŀ����ͼ��ʾ����ABC�����ԲԲ��O��AB�ϣ���D��BC�ӳ�����һ�㣬DM��AB��M����AC��N����AC=CD��CP����CDN��ND�ߵ����ߣ�
(1)��֤����ABC�ա�DNC��
(2)���ж�CP����O��λ�ù�ϵ����֤����Ľ��ۡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
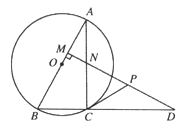
����Ŀ��Ϊ������Ӧ��ί���������������ʵ��ΰ���й��Σ����������³������ĺ��٣�����ijУ�ڰˣ����꼶��չ���Ļ��Уѧ������������꼶�����ڵ�Ͷ���������ͳ�ƣ����Ƴ�����ͼ��ʾ��������������ͳ��ͼ��
��1��������ͳ��ͼ��Ͷ��ƪ��Ϊ2����Ӧ�����ε�Բ�ĽǵĶ�����
��2�����У�ˣ����꼶��������һ����Ͷ���ƽ��ƪ��������������ͳ��ͼ����������
��3����Ͷ��ƪ��Ϊ9ƪ�������༶�У��ˣ����꼶���������࣬Уѧ�����������ĸ���ѡ��������μ�ȫ�еı��ûᣬ�������б�������״ͼ�ķ��������ѡ���������ò���ͬһ�꼶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B������ֱ�Ϊ��1��1���ͣ�5��4����������y=ax2+bx+c��a��0���Ķ������߶�AB���˶�����x�ύ��C��D���㣨C��D����ࣩ���������ߵĶ���ΪAʱ����C�ĺ�����ΪO�����D�ĺ��������ֵΪ�� ��

A��5 B��6 C��7 D��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x3��9x�ֽ���ʽ�������ȷ���ǣ� ��
A.x��x2��9��
B.x��x��3��2
C.x��x+3��2
D.x��x+3����x��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڶ�������ĺ�����l����һ��Ϊ1ǧ����ͷMN������ͷ����M����������30 ǧ�״���һ�۲�վO��ijʱ�̲��һ������ֱ�ߺ��е��ִ�λ��O�ı�ƫ��30�㷽������O���20![]() ǧ��A��������40���ӣ��ֲ�ø��ִ�λ��O��������������O���20ǧ��B����
ǧ��A��������40���ӣ��ֲ�ø��ִ�λ��O��������������O���20ǧ��B����
��1������ִ����е��ٶȣ�
��2��������ִ����ı亽��������У���ô�ִ��ܷ�����������ͷMN��������˵�����ɣ����ο����ݣ�![]() ��
��![]() ��
��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com