
【题目】如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20![]() 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据:![]() ,
,![]() )
)

【答案】(1)30千米/时;(2) 该轮船不改变航向继续航行,不能行至码头MN靠岸.
【解析】
试题分析:(1))过点A作AC⊥OB于点C.可知△ABC为直角三角形.根据勾股定理解答.
(2)延长AB交l于D,比较OD与AM、AN的大小即可得出结论.
试题解析:(1)过点A作AC⊥OB于点C.由题意,得
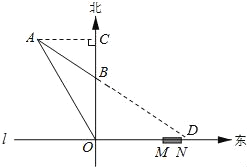
OA=![]() 千米,OB=20千米,∠AOC=30°.
千米,OB=20千米,∠AOC=30°.
∴![]() (千米).
(千米).
∵在Rt△AOC中,OC=OAcos∠AOC=![]() =30(千米).
=30(千米).
∴BC=OC-OB=30-20=10(千米).
∴在Rt△ABC中,![]() =20(千米).
=20(千米).
∴轮船航行的速度为:![]() (千米/时).
(千米/时).
(2)如果该轮船不改变航向继续航行,不能行至码头MN靠岸.
理由:延长AB交l于点D.
∵AB=OB=20(千米),∠AOC=30°.
∴∠OAB=∠AOC=30°,∴∠OBD=∠OAB+∠AOC=60°.
∴在Rt△BOD中,OD=OBtan∠OBD=20×tan60°=![]() (千米).
(千米).
∵![]() >30+1,
>30+1,
∴该轮船不改变航向继续航行,不能行至码头MN靠岸.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
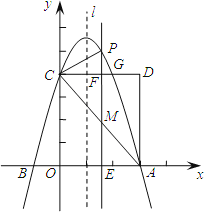
【题目】如图,抛物线![]() (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BE⊥AC于点E,AD⊥BC于点D,连接DE.

(1)若AB=BC,DE=1,BE=3,求△ABC的周长;
(2)如图2,若AB=BC,AD=BD,∠ADB的角平分线DF交BE于点F,求证:BF=![]() DE;
DE;
(3)如图3,若AB≠BC,AD=BD,将△ADC沿着AC翻折得到△AGC,连接DG、EG,请猜想线段AE、BE、DG之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+8x+9=0,变形后的结果正确的是( )
A. (x+4)2=﹣7 B. (x+4)2=﹣9 C. (x+4)2=7 D. (x+4)2=25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下命题是假命题的是( )
A. 对顶角相等 B. 经过直线外一点,有且只有一条直线与这条直线平行
C. 两直线被第三条直线所截,内错角相等 D. 邻补角是互补的角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com