
����Ŀ����ͼ����ABC�У�BE��AC�ڵ�E��AD��BC�ڵ�D������DE��

��1����AB=BC��DE=1��BE=3�����ABC���ܳ���
��2����ͼ2����AB=BC��AD=BD����ADB�Ľ�ƽ����DF��BE�ڵ�F����֤��BF=![]() DE��
DE��
��3����ͼ3����AB��BC��AD=BD������ADC����AC���۵õ���AGC������DG��EG��������߶�AE��BE��DG֮���������ϵ����֤����Ľ��ۣ�
���𰸡�(1) 2![]() +2����2��֤������������3��BE=DG+AE������������.
+2����2��֤������������3��BE=DG+AE������������.
��������
�����������1����ֱ��������б���ϵ��������ʵó�DE=![]() AC=AE��AC=2DE=2��AE=1���ɹ��ɶ������AB���ó�BC�����ɵó������
AC=AE��AC=2DE=2��AE=1���ɹ��ɶ������AB���ó�BC�����ɵó������
��2������AF���ɵ��������ε����ʵó���3=��4��֤����ABD�ǵ���ֱ�������Σ��ó���DAB=��DBA=45�㣬��3=22.5�㣬��ASA֤����ADF�ա�BDF���ó�AF=BF����2=��3=22.5�㣬֤����AEF�ǵ���ֱ�������Σ��ó�AF=![]() AE�����ɵó����ۣ�
AE�����ɵó����ۣ�
��3����DH��DE��BE��H����֤����ADE�ա�BDH���ó�DH=DE��AE=BH��֤����DHE�ǵ���ֱ�������Σ��ó���DEH=45�㣬��3=45�㣬�ɷ��۵����ʵó�DE=GE����3=��4=45�㣬֤��DH=GE��DH��GE��֤���ı���DHEG��ƽ���ı��Σ��ó�DG=EH�����ɵó����ۣ�
�����������1����ͼ1��ʾ��

��AB=BC��BE��AC��
��AE=CE����AEB=90�㣬
��AD��BC��
���ADC=90�㣬
��DE=![]() AC=AE��
AC=AE��
��AC=2DE=2��AE=1��
��AB=![]() ��
��
��BC=![]() ��
��
���ABC���ܳ�=AB+BC+AC=2![]() +2��
+2��
��2������AF����ͼ2��ʾ��
��AB=BC��BE��AC��
���3=��4��
�ߡ�ADC=90�㣬AD=BD��
���ABD�ǵ���ֱ�������Σ�
���DAB=��DBA=45�㣬
���3=22.5�㣬
�ߡ�1+��C=��3+��C=90�㣬
���1=��3=22.5�㣬
��DFƽ�֡�ABD��
���ADF=��BDF��
�ڡ�ADF�͡�BDF�У�
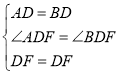 ��
��
���ADF�ա�BDF��SAS����
��AF=BF����2=��3=22.5�㣬
���EAF=��1+��2=45�㣬
���AEF�ǵ���ֱ�������Σ�
��AF=![]() AE��
AE��
��DE=AE��
��BF=![]() DE��
DE��
��3��BE=DG+AE���������£�
��DH��DE��BE��H����ͼ3��ʾ��
��BE��AC��AD��BC��
���1+��ACD=��2+��ACD=90�㣬
���1=��2��
���ADE=90��-��ADH=��BDH��
�ڡ�ADE�͡�BDH�У�
 ��
��
���ADE�ա�BDH��ASA����
��DH=DE��AE=BH��
���DHE�ǵ���ֱ�������Σ�
���DEH=45�㣬
���3=90��-��DEH=45�㣬
�ߡ�ACD��������ACG��
��DE=GE����3=��4=45�㣬
���DEG=��EDH=90�㣬DH=GE��
��DH��GE��
���ı���DHEG��ƽ���ı��Σ�
��DG=EH��
��BE=EH+BH=DG+AE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
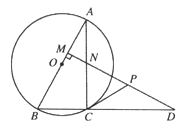
����Ŀ����ͼ��ʾ����ABC�����ԲԲ��O��AB�ϣ���D��BC�ӳ�����һ�㣬DM��AB��M����AC��N����AC=CD��CP����CDN��ND�ߵ����ߣ�
(1)��֤����ABC�ա�DNC��
(2)���ж�CP����O��λ�ù�ϵ����֤����Ľ��ۡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������A��1��m�����B��3��n������ֱ��y����2x+1�ϣ���ôm��n�Ĺ�ϵ�ǣ�������
A. m��nB. m��nC. m��nD. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������߳��ֱ�Ϊ2��9,�����ߵij�Ϊ���η���x2-14x+48=0��һ��, ����������ε��ܳ�Ϊ�� ��
A��11 B��17 C��17��19 D��19
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڶ�������ĺ�����l����һ��Ϊ1ǧ����ͷMN������ͷ����M����������30 ǧ�״���һ�۲�վO��ijʱ�̲��һ������ֱ�ߺ��е��ִ�λ��O�ı�ƫ��30�㷽������O���20![]() ǧ��A��������40���ӣ��ֲ�ø��ִ�λ��O��������������O���20ǧ��B����
ǧ��A��������40���ӣ��ֲ�ø��ִ�λ��O��������������O���20ǧ��B����
��1������ִ����е��ٶȣ�
��2��������ִ����ı亽��������У���ô�ִ��ܷ�����������ͷMN��������˵�����ɣ����ο����ݣ�![]() ��
��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������4�����⣺�����߶�Ӧ�ɱ������������������ƣ������߶�Ӧ�ɱ�����һ���Ƕ�Ӧ��ȵ��������������ƣ���һ����Ƕ�Ӧ��ȵ�����ֱ�����������ƣ���һ������ȵ������������������ƣ�������ȷ�������ǣ� ��
A. �٢� B. �٢� C. �٢ڢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com