
分析 (1)首先化简二次根式,进而合并同类二次根式得出答案;
(2)直接利用勾股定理求出b的值.
解答 解:(1)3$\sqrt{3}$-$\sqrt{8}$+$\sqrt{2}$-$\sqrt{27}$
=3$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{2}$-3$\sqrt{3}$
=-$\sqrt{2}$;
(2)∵直角三角形的斜边c=7,直角边a=4$\sqrt{3}$,
∴直角边b的长为:b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{{7}^{2}-(4\sqrt{3})^{2}}$=1.
点评 此题主要考查了二次根式的应用,正确化简二次根式是解题关键.


科目:初中数学 来源: 题型:解答题
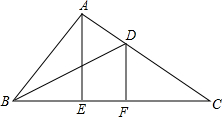 在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=4:7,BD平分∠ABC,点F在BC上,∠CDF=70°,∠ABD=25°.
在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=4:7,BD平分∠ABC,点F在BC上,∠CDF=70°,∠ABD=25°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图1,等边三角形ABC的边长为6,建立适当的直角坐标系,并写出各点的坐标.
(1)如图1,等边三角形ABC的边长为6,建立适当的直角坐标系,并写出各点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在8×8的方格纸中建立平面直角坐标系,已知A(2,4)、B(4,2).C是第一象限内的一个格点,且点C与线段AB可以组成一个以AB为底、腰长为无理数的等腰三角形.
如图,在8×8的方格纸中建立平面直角坐标系,已知A(2,4)、B(4,2).C是第一象限内的一个格点,且点C与线段AB可以组成一个以AB为底、腰长为无理数的等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王丽同学在计算122和892时,借助计算器探究“两位数的平方”有否简捷的计算方法.她经过探索并用计算器验证,再用数学知识解释,得出“两位数的平方”可用“竖式计算法”进行计算,如图,其中第一行的“01”和“04”分别是十位数和个位数的平方,各占两个位置,其结果不够两位的就在“十位”位置上放上“0”,再把它们并排 排列;第二行的“04”为十位数与个位数积的2倍,占两个位置,其结果不够两位的就在“十位”位置上放上“0”,再把它们按上面的竖式相加就得到了122=144.其中第一行的“64”和“81”分别是十位数和个位数的平方,各占两个位置,再把它们并排排列;第二行的“144”为十位数与个位数积的2倍,再把它们按上面的竖式相加就得到了892=7921.
王丽同学在计算122和892时,借助计算器探究“两位数的平方”有否简捷的计算方法.她经过探索并用计算器验证,再用数学知识解释,得出“两位数的平方”可用“竖式计算法”进行计算,如图,其中第一行的“01”和“04”分别是十位数和个位数的平方,各占两个位置,其结果不够两位的就在“十位”位置上放上“0”,再把它们并排 排列;第二行的“04”为十位数与个位数积的2倍,占两个位置,其结果不够两位的就在“十位”位置上放上“0”,再把它们按上面的竖式相加就得到了122=144.其中第一行的“64”和“81”分别是十位数和个位数的平方,各占两个位置,再把它们并排排列;第二行的“144”为十位数与个位数积的2倍,再把它们按上面的竖式相加就得到了892=7921.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com