
【题目】抛物线y=4x2﹣2ax+b与x轴相交于A(x1 , 0),B(x2 , 0)(0<x1<x2)两点,与y轴交于点C.
(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
【答案】
(1)
解:∵tan∠ABC=4
∴可以假设B(m,0),则A(m﹣2,0),C(0,4m),
∴可以假设抛物线的解析式为y=4(x﹣m)(x﹣m+2),
把C(0,4m)代入y=4(x﹣m)(x﹣m+2),得m=3,
∴抛物线的解析式为y=4(x﹣3)(x﹣1),
∴y=4x2﹣16x+12
(2)
解:如图,设P(m,4m2﹣16m+12).作PH∥OC交BC于H.
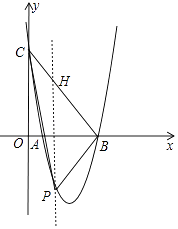
∵B(3,0),C(0,12),
∴直线BC的解析式为y=﹣4x+12,
∴H(m,﹣4m+12),
∴S△PBC=S△PHC+S△PHB= ![]() (﹣4m+12﹣4m2+16m﹣12)3=﹣6(m﹣
(﹣4m+12﹣4m2+16m﹣12)3=﹣6(m﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣6<0,
∴m= ![]() 时,△PBC面积最大,
时,△PBC面积最大,
此时P( ![]() ,﹣3)
,﹣3)
(3)
解:不存在.
理由:假设存在.由题意可知,
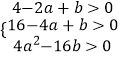 且1<﹣
且1<﹣ ![]() <2,
<2,
∴4<a<8,
∵a是整数,
∴a=5 或6或7,
当a=5时,代入不等式组,不等式组无解.
当a=6时,代入不等式组,不等式组无解.
当a=7时,代入不等式组,不等式组无解.
综上所述,不存在整数a、b,使得1<x1<2和1<x2<2同时成立
【解析】(1)由tan∠ABC=4,可以假设B(m,0),则A(m﹣2,0),C(0,4m),可得抛物线的解析式为y=4(x﹣m)(x﹣m+2),把C(0,4m)代入y=4(x﹣m)(x﹣m+2),求出m的值即可解决问题;(2)设P(m,4m2﹣16m+12).作PH∥OC交BC于H,根据S△PBC=S△PHC+S△PHB构建二次函数,理由二次函数的性质解决问题;(3)不存在.假设存在,由题意由题意可知, 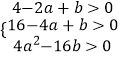 且1<﹣
且1<﹣ ![]() <2,首先求出整数a的值,代入不等式组,解不等式组即可解决问题.
<2,首先求出整数a的值,代入不等式组,解不等式组即可解决问题.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
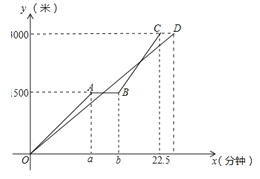
【题目】(2017黑龙江省齐齐哈尔市,第25题,10分)“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人再次选择自行车作为出行工具,小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)a= ,b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是v米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.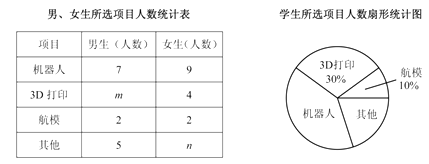
根据以上信息解决下列问题:
(1)![]() ,
, ![]() ;
;![]()
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的 ![]() 名学生中随机选取
名学生中随机选取 ![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的 ![]() 名学生中恰好有
名学生中恰好有 ![]() 名男生、
名男生、 ![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
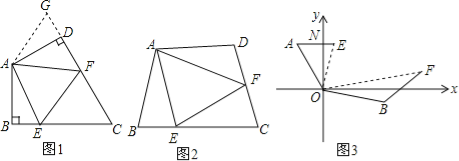
【题目】如图1,已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点D是BC的中点
,点D是BC的中点![]() 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
![]() 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______;
![]() 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转![]() ,
,
![]() 判断
判断![]() 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论;
![]() 若
若![]() ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(13分)(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD= ![]() ∠BAC=60°,于是
∠BAC=60°,于是 ![]() =
= ![]() =
= ![]() ; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.
; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.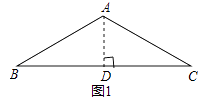
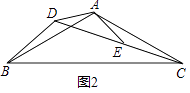
(1)①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;
(2)拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF. 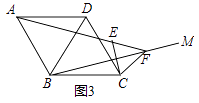
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.

(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC. 
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com