
����Ŀ����2017������ʡ��������У���25�⣬10�֣�����̼��������ɫ������������õ����Ⱥ�ڵĽ��ܣ�Խ��Խ������ٴ�ѡ�����г���Ϊ���й��ߣ�С���Ͱְ�ͬʱ�Ӽ������г�ȥͼ��ݣ��ְ�����150��/�ֵ��ٶ�����һ��ʱ�䣬��Ϣ��5���ӣ�����m��/�ֵ��ٶȵ���ͼ��ݣ�С��ʼ����ͬһ�ٶ����У�������ʻ��·��y���ף���ʱ��x�����ӣ��Ĺ�ϵ��ͼ������ͼ����������⣺
��1��a= ��b= ��m= ��
��2����С�����ٶ���120��/�֣���С����;����ְֵڶ�������ʱ����ͼ��ݵľ��룻
��3���ڣ�2���������£��ְ��Եڶ��γ���������ͼ���ǰ����ʱ��С�����100�ף�
��4����С������ʻ�ٶ���v��/�֣�����;����ְ�ǡ���������Σ��������ҡ�ͼ������أ�����ֱ��д��v��ȡֵ��Χ��
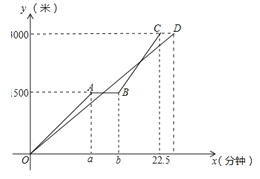
���𰸡���1��10��15��200����2��750�ף���3��17.5����ʱ��20���ӣ���4��100��v��![]() ��
��
�����������⣨1������ʱ��=·�����ٶȣ��������aֵ�������Ϣ��ʱ��Ϊ5���ӣ����ɵó�bֵ���ٸ����ٶ�=·����ʱ�䣬�������m��ֵ��
��2������������ϵ�ҳ��߶�BC��OD����ֱ�ߵĺ�������ʽ����������������ʽ�ɷ����飬ͨ���ⷽ���������������꣬����3000ȥ������������꣬���ɵó����ۣ�
��3�����ݣ�2�����۽�϶���֮�����100�ף����ɵó�����x�ĺ�����ֵ���ŵ�һԪһ�η��̣���֮���ɵó����ۣ�
��4���ֱ������OD����B��Cʱ��С�����ٶȣ����ͼ�Σ��������ν�ϼ��ɵó����ۣ�
�����������1��a=1500��150=10�����ӣ���
b=10+5=15�����ӣ���
m=(3000-1500)����22.5��15��=200����/�֣���
�ʴ�Ϊ��10��15��200��
��2���߶�BC����ֱ�ߵĺ�������ʽΪy=1500+200��x��15��=200x��1500��
�߶�OD���ڵ�ֱ�ߵĺ�������ʽΪy=120x��
��������������ʽ�ɷ����飬![]() ����ã�
����ã� ��
��
��3000��2250=750���ף���
��С����;����ְֵڶ�������ʱ����ͼ��ݵľ�����750�ף�
��3����������ã�|200x��1500��120x|=100��
��ã�x1=![]() =17.5��x2=20��
=17.5��x2=20��
�𣺰ְ��Եڶ��γ���������ͼ���ǰ��17.5����ʱ��20����ʱ��С�����100�ף�
��4�����߶�OD����Bʱ��С�����ٶ�Ϊ1500��15=100����/���ӣ���
���߶�OD����Cʱ��С�����ٶ�Ϊ3000��22.5=![]() ����/���ӣ���
����/���ӣ���
���ͼ�ο�֪����100��v��![]() ʱ��С����;����ְ�ǡ���������Σ��������ҡ�ͼ������أ���
ʱ��С����;����ְ�ǡ���������Σ��������ҡ�ͼ������أ���




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ѿ�ѧϰ������������y= ![]() ��ͼ������ʣ���ع��о����Ĺ��̣��Ժ���y=
��ͼ������ʣ���ع��о����Ĺ��̣��Ժ���y= ![]() ����̽�������н��ۣ�
����̽�������н��ۣ�
��ͼ���ڵ�һ�������ޣ���ͼ���ڵ�һ�������ޣ�
��ͼ�����y��Գƣ���ͼ�����ԭ��Գƣ�
�ݵ�x��0ʱ��y��x���������x��0ʱ��y��x���������
��x��0ʱ��y��x�������С����x��0ʱ��y��x���������
�Ǻ���y= ![]() �����ʼ�����ͼ���������ǣ� �� ����д������ȷ�𰸵���ţ�
�����ʼ�����ͼ���������ǣ� �� ����д������ȷ�𰸵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ABC��,��C=90��,BEƽ�֡�ABC,��AC���ڵ�E,ED��AB,����ΪD.����ABC���ܳ�Ϊ12,��ADE���ܳ�Ϊ6,��BC�ij�Ϊ�� ��

A. 3 B. 4 C. 5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������һ�ֲ�Ʒ�����ֲ�Ʒ�ijɱ���Ϊ10Ԫ/ǧ�ˣ��г����鷢�֣��ò�Ʒÿ���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ���10��x��18��֮��ĺ�����ϵ��ͼ��ʾ��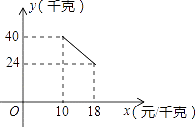
��1����y��ǧ�ˣ������ۼ�x�ĺ�����ϵʽ��
��2���þ�������Ҫ���150Ԫ�������������ۼ�Ӧ��Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��ѧУ��֯���������и����˽�������ס��С��450�������������ˮ��������������������50��������¾���ˮ��(��λ��t)����������������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ(��ͼ)��
(1)������������е���Ϣ��ȫƵ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
�¾���ˮ��/t | Ƶ�� | �ٷֱ� |
2��x��3 | 2 | 4% |
3��x��4 | 12 | 24% |
4��x��5 | ||
5��x��6 | 10 | 20% |
6��x��7 | 12% | |
7��x��8 | 3 | 6% |
8��x��9 | 2 | 4% |
 ��
��
(2)�����ͥ�¾���ˮ�������ڻ����4 t��С��7 t��Ϊ�е���ˮ����ͥ������ͨ���������������е��е���ˮ����ͥ��Լ�ж��ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���C������Ϊ��4����1����
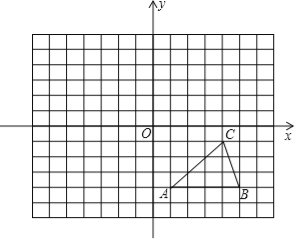
��1������ABC����ƽ��5����λ��õ���Ӧ����A1B1C1��������A1B1C1����д��C1�����ꣻ
��2����ԭ��OΪ�Գ����ģ��ٻ�������A1B1C1����ԭ��O�ԳƵ���A2B2C2����д����C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ10��B��������λ�ڵ�A���һ������AB=30������P�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊ![]() ��.
��.
![]()
(1)�����ϵ�B��ʾ������________����P��ʾ������________(�ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
(2)��MΪ�߶�AP���е���NΪ�߶�BP���е����ڵ�P�˶��Ĺ��������߶�MN�ij��Ȼᷢ���仯��?����������������������������仯,���ú�![]() �Ĵ���ʽ��ʾ���������
�Ĵ���ʽ��ʾ���������
(3)����Q�ӵ�B����������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������ʵ�P�˶�������ʱ���Q���4����λ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=4x2��2ax+b��x���ཻ��A��x1 �� 0����B��x2 �� 0����0��x1��x2�����㣬��y�ύ�ڵ�C��
��1����AB=2��tan��ABC=4����������ߵĽ���ʽ��
��2���ڣ�1���У�����DΪֱ��BC�·���������һ���㣬����BCD��������ʱ�����D�����ꣻ
��3���Ƿ��������a��bʹ��1��x1��2��1��x2��2ͬʱ��������֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com