
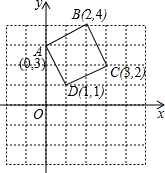
 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针方向旋转90°后,B点的坐标为(4,0);△DCB扫过的面积为$\frac{5}{2}$π+$\frac{5}{2}$.
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针方向旋转90°后,B点的坐标为(4,0);△DCB扫过的面积为$\frac{5}{2}$π+$\frac{5}{2}$. 分析 利用网格特点和旋转的性质画出正方形ABCD绕D点顺时针方向旋转90°后所得的正方形CEFD,则可得到B点的对应点的坐标,再利用勾股定理计算出BD、DF,然后根据扇形面积公式,利用△DCB扫过的面积=S扇形DBE+S△EDF进行计算即可.
解答 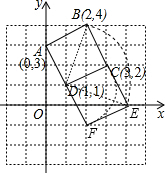 解:如图,正方形ABCD绕D点顺时针方向旋转90°后得到正方形CEFD,则B点旋转后的对应点为E(4,0),
解:如图,正方形ABCD绕D点顺时针方向旋转90°后得到正方形CEFD,则B点旋转后的对应点为E(4,0),
BD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,EF=DF=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
△DCB扫过的面积=S扇形DBE+S△EDF=$\frac{90•π•(\sqrt{10})^{2}}{360}$+$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$=$\frac{5}{2}$π+$\frac{5}{2}$.
故答案为(4,0),$\frac{5}{2}$π+$\frac{5}{2}$.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
| 正面 | -(-1) | |-2| | (-1)3 | 0 | -3 | +5 |
| 背面 | a | h | k | n | s | t |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
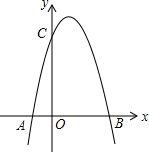 如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(-1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
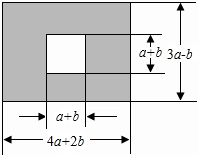 眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.
眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
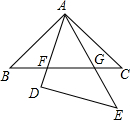 如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.
如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
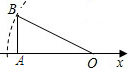 如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | -2 | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=6cm,则线段AC=24 cm.
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=6cm,则线段AC=24 cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com