
【题目】某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)

【答案】施工方提供的设计方案不满足安全要求.
【解析】试题分析:
在Rt△ABC中,由∠ACB=90°,AC=15m,∠ABC=45°可求得BC=15m;在Rt△EGD中,由∠EGD=90°,EG=15m,∠EFG=37°,可解得GF=20m;通过已知条件可证得四边形EACG是矩形,从而可得GC=AE=2m;这样可解得:DF=GC+BC+BD-GF=2+15+5-20=2<2.5,由此可知:“设计方案不满足安全要求”.
试题解析:
施工方提供的设计方案不满足安全要求,理由如下:
在Rt△ABC中,AC=15m,∠ABC=45°,
∴BC=![]() =15m.
=15m.
在Rt△EFG中,EG=15m,∠EFG=37°,
∴GF=![]() ≈
≈![]() =20m.
=20m.
∵EG=AC=15m,AC⊥BC,EG⊥BC,
∴EG∥AC,
∴四边形EGCA是矩形,
∴GC=EA=2m,
∴DF=GC+BC+BD-GF=2+15+5-20=2<2.5.
∴施工方提供的设计方案不满足安全要求.


科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),在正方形一边上取中点,并沿虚线剪开,用两块图形拼一拼,能否拼出平行四边形、梯形或三角形?画图解释你的判断.
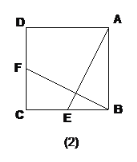
(2)如图(2)E为正方形ABCD边BC的中点,F为DC的中点,BF与AE有何关系?请解释你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,以BF为底向正方形外侧作等腰直角三角形BEF,连接DF,取DF的中点G,连接EG,CG.

(1)如图1,当点A与点F重合时,猜想EG与CG的数量关系为 ,EG与CG的位置关系为 ,请证明你的结论.
(2)如图2,当点F在AB上(不与点A重合)时,(1)中结论是否仍然成立?请说明理由;如图3,点F在AB的左侧时,(1)中的结论是否仍然成立?直接做出判断,不必说明理由.
(3)在图2中,若BC=4,BF=3,连接EC,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC,∠3=∠B,则∠1+∠2=180°.下面是王宁同学的思考过程,请你在括号内填上理由、依据或内容。

思考过程
因为 DE∥BC(已知)
所以∠3=∠EHC ( )
因为∠3=∠B(已知)
所以∠B=∠EHC ( )
所以 AB∥EH ( )
∠2+ ( )=180°( )
因为∠1=∠4( )
所以∠1+∠2=180°(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=______度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角尺按图①所示的方式叠放在一起,现将含45°角的三角尺ADE固定不动,把含30°角的三角尺ABC绕顶点A顺时针旋转角α(α=∠BAD且0°<α<180°),使两块三角尺至少有一组边平行.


(1)如图②,当α=________°时,BC∥DE.
(2)请你分别在图③,④中,各画一种符合要求的图形,标出α,并完成下列各题.
图③中,当α=________°时,________∥________;
图④中,当α=________°时,________∥________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了扩大生产,决定购买8台机器用于生产零件,现有甲、乙两种机器可供选择,其中甲型机器每日生产零件100个,乙型机器每日生产零件60个,经调查,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂买机器的预算资金不超过46万元,那么该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的8台机器生产零件的日产量不低于550个,那么为了节约资金,应该选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com