
科目:初中数学 来源: 题型:解答题
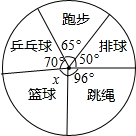 如图,这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图,但负责画此图的同学忘记了最喜爱篮球运动的人数.
如图,这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图,但负责画此图的同学忘记了最喜爱篮球运动的人数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
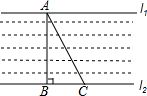 如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$cm,3πcm2 | B. | 2$\sqrt{2}$cm,3πcm2 | C. | 2$\sqrt{2}$cm,6πcm2 | D. | $\sqrt{10}$cm,6πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
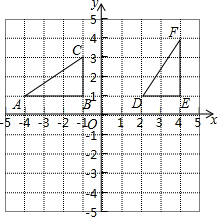 如图,△ABC和△DEF在直角坐标系中的位置如图所示.
如图,△ABC和△DEF在直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
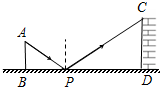 如图是孔明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD,且测得AB=6米,BP=9米,PD=15米,那么该古城墙的高度是( )
如图是孔明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知 AB⊥BD,CD⊥BD,且测得AB=6米,BP=9米,PD=15米,那么该古城墙的高度是( )| A. | 6米 | B. | 8米 | C. | 10米 | D. | 15米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com