
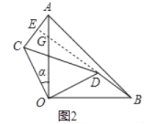
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
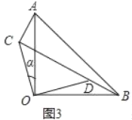
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.

【答案】(1)证明见解析;(2)AC=7, ![]()
【解析】试题分析:(1)图形经过旋转以后,明确没有变化的边长,根据全等三角形的判定定理证明图中的△COA≌△DOB,从而证明AC=BD,做辅助△ABE,证明∠AEB=90°,从而得到AC⊥BD;
(2)在△COA中,根据余弦定理,得出cosα的值,从而求出sinα的值.
试题解析:(1)如图2中,延长BD交OA于G,交AC于E.
∵∠AOB=∠COD=90°,
∴∠AOC=∠DOB,
在△AOC和△BOD中, 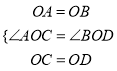 ,
,
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
∵∠DBO+∠GOB=90°,
∵∠OGB=∠AGE,
∴∠CAO+∠AGE=90°,
∴∠AEG=90°,
∴BD⊥AC.
(2)如图3中,设AC=x,
∵BD、CD在同一直线上,BD⊥AC,
∴△ABC是直角三角形,
∴AC2+BC2=AB2,
∴x2+(x+17)2=252,
解得x=7,
∵∠ODC=∠α+∠DBO=45°,∠ABC+∠DBO=45°,
∴∠α=∠ABC,
∴sinα=sin∠ABC=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“圆内接四边形的对角互补”是随机事件
B.任意掷一枚质地均匀的硬币10次,正面朝上的次数不一定是5次
C.天气预报明天下雨的概率是99%,说明明天一定会下雨
D.“三点确定一个圆”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: ![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() ,请回答问题:
,请回答问题:
(![]() )请直接写出
)请直接写出![]() 、
、![]() 、
、![]() 的值:
的值: ![]() __________,
__________, ![]() __________,
__________, ![]() __________.
__________.
(![]() )数轴上
)数轴上![]() ,
, ![]() ,
, ![]() 所对应的点分别为
所对应的点分别为![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() ,
, ![]() 之间的一个动点,其对应的数为
之间的一个动点,其对应的数为![]() ,请化简
,请化简![]() (请写出化简过程).
(请写出化简过程).
(![]() )在(
)在(![]() )、(
)、(![]() )的条件下,点
)的条件下,点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动.同时,点
个单位长度的速度向左运动.同时,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,假设
个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .请问:
.请问: ![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF. 
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,BC、AD是⊙O的切线,过O点作EC⊥OD,EC交BC于C,交直线AD于E.
(1)求证:CD是⊙O的切线;
(2)若AE=1,AD=3,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC内任意一点P(x0,y0),将三角形ABC平移后,点P的对应点为P1(x0+5,y0-3).
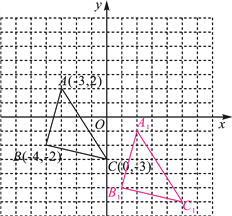
(1)写出将三角形ABC平移后,三角形ABC中A,B,C分别对应的点A1,B1,C1的坐标,并画出三角形A1B1C1;
(2)若三角形ABC外有一点M经过同样的平移后得到点M1(5,3),写出M点的坐标_______,若连接线段MM1,PP1,则这两条线段之间的关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有35名同学参加眉山市的三苏文化知识竞赛,预赛分数各不相同,取前18名同学参加决赛. 其中一名同学知道自己的分数后,要判断自己能否进入决赛,只需要知道这35名同学分数的( ).
A. 众数 B. 中位数 C. 平均数 D. 方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com