
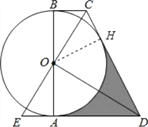
【题目】如图,AB为⊙O的直径,BC、AD是⊙O的切线,过O点作EC⊥OD,EC交BC于C,交直线AD于E.
(1)求证:CD是⊙O的切线;
(2)若AE=1,AD=3,求阴影部分的面积.

【答案】(1)见解析;(2) 3![]() ﹣π;
﹣π;
【解析】试题分析:(1)首先作OH⊥CD,垂足为H,由BC、AD是⊙O的切线,易证得△BOC≌△AOE(ASA),继而可得OD是CE的垂直平分线,则可判定DC=DE,即可得OD平分∠CDE,则可得OH=OA,证得CD是⊙O的切线;
(2)首先证得△AOE∽△ADO,然后由相似三角形的对应边成比例,求得OA的长,然后利用三角函数的性质,求得∠DOA的度数,继而求得答案.
试题解析:
(1)证明:作OH⊥CD,垂足为H,
∵BC、AD是⊙O的切线,
∴∠CBO=∠OAE=90°,
在△BOC和△AOE中,![]() ,
,
∴△BOC≌△AOE(ASA),
∴OC=OE,
又∵EC⊥OD,
∴DE=DC,
∴∠ODC=∠ODE,
∴OH=OA,
∴CD是⊙O的切线;
(2)∵∠E+∠AOE=90°,∠DOA+∠AOE=90°,
∴∠E=∠DOA,
又∵∠OAE=∠ODA=90°,
∴△AOE∽△ADO,
∴![]() =
=![]() ,
,
∴OA2=EAAD=1×3=3,
∵OA>0,
∴OA=![]() ,
,
∴tanE=![]() =
=![]() ,
,
∴∠DOA=∠E=60°,
∵DA=DH,∠OAD=∠OHD=90°,
∴∠DOH=∠DOA=60°,
∴S阴影部分=![]() ×3×
×3×![]() +
+![]() ×3×
×3×![]() ﹣
﹣![]() =3
=3![]() ﹣π.
﹣π.


科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.长度相等的弧是等弧
B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.圆的切线垂直于这个圆的半径
D.90°的圆周角所对的弦是圆的直径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,老师出示了这样一道题目:“如图,BD是矩形ABCD的对角线,将AB沿BE折叠,使A点落在BD上的点G处,将边CD沿DF折叠,使点C落在BD上的点H处,求证:四边形BEDF是平行四边形”.小丽选择了先证明△DEG≌△BFH,再证明DE=BF,进而得到四边形BEDF是平行四边形,小明向老师提出了另一种证明方法.
(1)小丽证明四边形BEDF是平行四边形的依据是;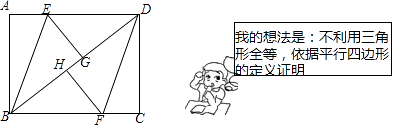
(2)按小明的想法写出证明过程;
(3)当学生们完成了证明后,老师又提出如下问题,连接EH,FG,若AB=6,BC=8,试求四边形EGFH的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( ) 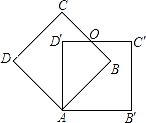
A.![]()
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球上的陆地面积约为149000000平方千米,这个数字用科学记数法表示应为( )
A.0.149×106
B.1.49×107
C.1.49×108
D.14.9×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com