
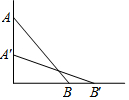
 如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.
如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.分析 (1)分别在在Rt△ABO中和在Rt△A′OB′中,求出OA、OA′即可解决问题.
(2)点P运动轨迹是弧,求出圆心角、半径利用弧长公式计算即可.
解答 解:(1)在Rt△ABO中,∵AB=a,∠ABO=α,
∴OA=AB•sinα=a•sinα,
在Rt△A′OB′中,同理可得OA′=a•sinβ,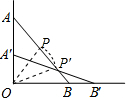
∴AA′=OA-OA′=a(sinα-sinβ).
故答案为a(sinα-sinβ).
(2)∵PA=PB,∠AOB=90°,
∴OP=PB=PA,
∴∠POB=α,同理可得∠P′OB=β,
∴∠POP′=α-β,
∴则点P所经过的路线长=$\frac{(α-β)π•\frac{1}{2}a}{180}$=$\frac{(α-β)•π•a}{360}$.
点评 本题考查勾股定理、轨迹、弧长公式、直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
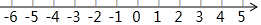 解不等式(组),并把第(2)的解集表示在数轴上.
解不等式(组),并把第(2)的解集表示在数轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
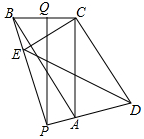 如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求:
如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
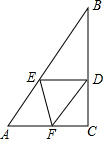 如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.
如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com