
如图,在 中,AB=AC,以AB为直径的
中,AB=AC,以AB为直径的 交BC于点M,
交BC于点M,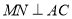 于点N.
于点N.

(1)求证:MN是⊙O的切线;
(2)若 ,AB=2,求图中阴影部分的面积.
,AB=2,求图中阴影部分的面积.
(1)证明见解析;(2)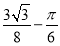 .
.
【解析】
试题分析:(1)有切点,需连半径,证明垂直,即可;
(2)求阴影部分的面积要把它转化成S梯形ANMO-S扇形OAM,再分别求的这两部分的面积求解.
试题解析:(1)证明:连接OM.
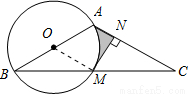
∵OM=OB,
∴∠B=∠OMB.
∵AB=AC,
∴∠B=∠C.
∴∠OMB=∠C.
∴OM∥AC.
∵MN⊥AC,
∴OM⊥MN.
∵点M在⊙O上,
∴MN是⊙O的切线.
(2)【解析】
连接AM.
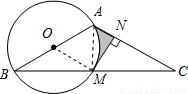
∵AB为直径,点M在⊙O上,
∴∠AMB=90°.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∴∠AOM=60°.
又∵在Rt△AMC中,MN⊥AC于点N,
∴∠AMN=30°.
∴AN=AM•sin∠AMN=AC•sin30°•sin30°=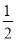 .
.
∴MN=AM•cos∠AMN=AC•sin30°•cos30°=
∴S梯形ANMO= ,S扇形OAM=
,S扇形OAM= ,
,
∴S阴影=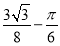 .
.
考点: 切线的判定;扇形面积的计算;解直角三角形.


科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:填空题
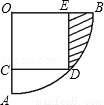
如图,扇形AOB的圆心角为直角,正方形OCDE内接于扇形,点C、E、D分别在OA、OB、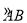 上,如果正方形的边长为1,那么阴影部分的面积为 .
上,如果正方形的边长为1,那么阴影部分的面积为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省黄冈市中考模拟考试数学试卷A(解析版) 题型:选择题
下列条件中,不能判定四边形ABCD是平行四边形的是 ( ).
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省黄冈市九年级下学期入学考试数学试卷(解析版) 题型:填空题
某地预估2014年全年旅游综合收入909600000元.数909600000用科学记数法表示(保留三个有效数字)为
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省鄂州市九年级4月调研考试数学试卷(解析版) 题型:填空题
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为____________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:解答题
已知抛物线 经过点A(3,2),B(0,1)和点C
经过点A(3,2),B(0,1)和点C .
.
(1)求抛物线的解析式;
(2)如图,若抛物线的顶点为P,点A关于对称轴的对称点为M,过M的直线交抛物线于另一点N(N在对称轴右边),交对称轴于F,若 ,求点F的坐标;
,求点F的坐标;
(3)在(2)的条件下,在y轴上是否存在点G,使△BMA与△MBG相似?若存在,求点G的坐标;若不存在,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com