
已知抛物线 经过点A(3,2),B(0,1)和点C
经过点A(3,2),B(0,1)和点C .
.
(1)求抛物线的解析式;
(2)如图,若抛物线的顶点为P,点A关于对称轴的对称点为M,过M的直线交抛物线于另一点N(N在对称轴右边),交对称轴于F,若 ,求点F的坐标;
,求点F的坐标;
(3)在(2)的条件下,在y轴上是否存在点G,使△BMA与△MBG相似?若存在,求点G的坐标;若不存在,请说明理由.


(1)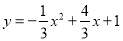 ;
;
(2)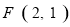 ;
;
(3)点G的坐标为(0,0)或(0,-1).
【解析】
试题分析:(1)根据图象可得出A、B、C三点的坐标,然后用待定系数法即可求出抛物线的解析式;
(2)求出M、N点坐标,根据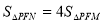 可得到N点坐标,根据直线MN的解析式可以求出M点坐标;
可得到N点坐标,根据直线MN的解析式可以求出M点坐标;
(3)分当△AMB∽△MBG时,当△BMA∽△MBG时,两种情况讨论即可.
试题解析:(1)由题得c=1,
∵抛物线过点A(3,2)和点C


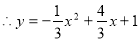 ;
;
(2)
∴P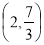 ,
,
 抛物线的对称轴为直线
抛物线的对称轴为直线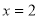 ,
,
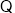 A与M关于对称轴对称
A与M关于对称轴对称
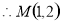 ,
,  ,
,
过点N作 于点H
于点H
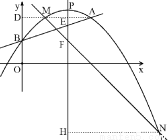
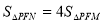
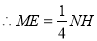
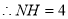
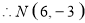 .
.
可求直线MN:y = - x+3
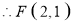 ;
;
(3)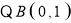 ,
,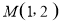 ,延长AM交y轴于点D,则D(0,2).
,延长AM交y轴于点D,则D(0,2).
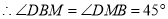 ,
,
 ,
,
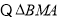 与
与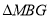 相似
相似
 点B与点M对应,点G只能在点B下方.
点B与点M对应,点G只能在点B下方.
设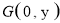
当△AMB∽△MBG时,

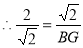
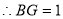
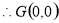 ,
,
当△BMA∽△MBG时,
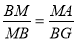
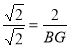
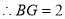
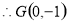
综上所述,满足要求的点G的坐标为(0,0)或(0,-1).
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年湖北省黄冈市九年级下学期入学考试数学试卷(解析版) 题型:解答题
如图,在 中,AB=AC,以AB为直径的
中,AB=AC,以AB为直径的 交BC于点M,
交BC于点M, 于点N.
于点N.

(1)求证:MN是⊙O的切线;
(2)若 ,AB=2,求图中阴影部分的面积.
,AB=2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:选择题
如图,梯形ABCD中,AD∥BC,AB=3,BC=4,连结BD,∠BAD的平分线交BD于 点E,且AE∥CD,则AD的长为( )
A.1 B.2 C.3 D.4

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:选择题
如图,AB∥CD,BC∥DE,若∠B=40°,则∠D的度数是( )
A.40° B.140° C.160° D.60°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:解答题
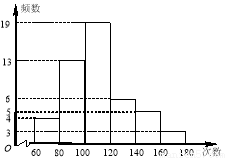
某中学对全校学生1分钟跳绳的次数进行了统计,全校1分钟跳绳的平均次数是100次.某班体育委员统计了全班50名学生1分钟跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点).
(1)求该班学生中跳绳次数达到或超过校平均水平的占全班人数的百分比;
(2)该班1分钟跳绳的平均次数至少是多少?是否超过全校平均次数?
(3)已知该班成绩最好的三名学生中有一名男生和两名女生,现要从三人中随机抽取两人参加学校举行的跳绳比赛,用列表或画树状图的方法求恰好抽到一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:解答题
在一个不透明的盒子里,装有四个分别标有数字 ,
, ,
, ,
, 的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(x,y)落在一次函数 的图象上的概率;
的图象上的概率;
(3)求小强、小华各取一次小球所确定的数x、y满足 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com