
【题目】如图,点A、B分别在x轴的负半轴和y轴的正半轴上,点C(2,﹣2),CA、CB分别交坐标轴于D、E,CA⊥AB,且CA=AB
(1)求点B的坐标;
(2)如图2,连接DE,求证:BD﹣AE=DE;
(3)如图3,若点F为(4,0),点P在第一象限内,连接PF,过P作PM⊥PF交y轴于点M,在PM上截取PN=PF,连接PO、BN,过P作∠OPG=45°交BN于点G,求证:点G是BN的中点.

【答案】(1)B(0,4);(2)见解析;(3)见解析
【解析】
(1)作CM⊥x轴于M,求出CM=CN=2,证△BAO≌△ACM,推出AO=CM=2,OB=AM=4,即可得出答案;
(2)在BD上截取BF=AE,连AF,证△BAF≌△CAE,证△AFD≌△CED,即可得出答案.
(3)作EO⊥OP交PG的延长线于E,连接EB、EN、PB,只要证明四边形ENPB是平行四边形就可以了.
解:(1)作CM⊥x轴于M,
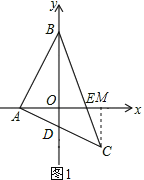
∵C(2,﹣2),
∴CM=2,OM=2,
∵AB⊥AC,
∴∠BAC=∠AOB=∠CMA=90°,
∴∠BAO+∠CAM=90°,∠CAM+∠ACM=90°,
∴∠BAO=∠ACM,
在△BAO和△ACM中,
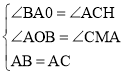 ,
,
∴△BAO≌△ACM,
∴AO=CM=2,OB=AM=AO+OM=2+2=4,
∴B(0,4).
(2)证明:在BD上截取BF=AE,连AF,

∵△BAO≌△CAM,
∴∠ABF=∠CAE,
在△ABF和△ACE中,
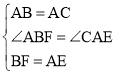 ,
,
∴△ABF≌△CAE(SAS),
∴AF=CE,∠ACE=∠BAF=45°,
∵∠BAC=90°,
∴∠FAD=45°=∠ECD,
由(1)可知OA=OM,OD∥CM,
∴AD=DC,(图1中),
在△AFD和△CED中,
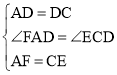 ,
,
∴△AFD≌△CED(SAS),
∴DE=DF,
∴BD﹣AE=DE;
(3)如图3,作EO⊥OP交PG的延长线于E,连接EB、EN、PB,
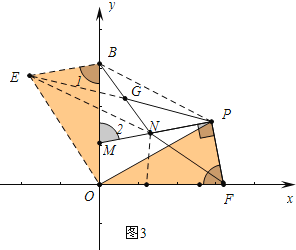
∵∠EOP=90°,∠EPO=45°,
∴∠OEP=∠EPO=45°,
∴EO=PO,
∵∠EOP=∠BOF=90°,
∴∠EOB=∠POF,
在△EOB和△POF中,
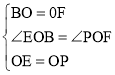 ,
,
∴△EOB≌△POF,
∴EB=PF=PN,∠1=∠OFP,
∵∠2+∠PMO=180°,
∵∠MOF=∠MPF=90°,
∴∠OMP+∠OFP=180°,
∴∠2=∠OFP=∠1,
∴EB∥PN,
∵EB=PN,
∴四边形ENPB是平行四边形,
∴BG=GN,
即点G是BN中点.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标平面上的![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .若抛物线
.若抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.

![]() 求
求![]() 、
、![]() 的值;
的值;
![]() 将抛物线向上平移若干个单位得到的新抛物线恰好经过点
将抛物线向上平移若干个单位得到的新抛物线恰好经过点![]() ,求新抛物线的解析式;
,求新抛物线的解析式;
![]() 设
设![]() 中的新抛物的顶点
中的新抛物的顶点![]() 点,
点,![]() 为新抛物线上
为新抛物线上![]() 点至
点至![]() 点之间的一点,以点
点之间的一点,以点![]() 为圆心画图,当
为圆心画图,当![]() 与
与![]() 轴和直线
轴和直线![]() 都相切时,联结
都相切时,联结![]() 、
、![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图E在△ABC的边AC上,且∠AEB=∠ABC.
⑴求证:∠ABE=∠C;
⑵若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=4,BD=3,求△ADE的周长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(0,2),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3![]() ,则点B′的坐标为( )
,则点B′的坐标为( )

A. (2![]() ,4) B. (2
,4) B. (2![]() ,3) C. (3
,3) C. (3![]() ,4) D. (3
,4) D. (3![]() ,3)
,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD.BC∥AD.
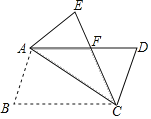
(1)求证:△ABC≌△CDA;
(2)△ABC关于对角线AC的对称图形为△AEC,EC、AD交于点F,判断△ACF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
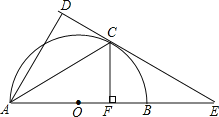
【题目】如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若BE=2,CE=2![]() ,CF⊥AB,垂足为点F.
,CF⊥AB,垂足为点F.
①求⊙O的半径;②求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com