
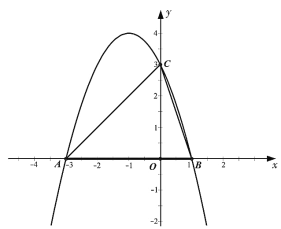
【题目】如图,抛物线与![]() 轴相交于点
轴相交于点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一动点, 联结
是抛物线上一动点, 联结![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)求这条抛物线的解析式,并写出顶点坐标;
(2)求![]() 的正切值;
的正切值;
(3)当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)2;(3)点
;(2)2;(3)点![]() 的坐标为
的坐标为 或
或![]()
【解析】
(1)利用待定系数法确定函数解析式,根据函数解析式求得该抛物线的顶点坐标;
(2)如图,过点B作BH⊥AC于点H,构造等腰直角△ABH和直角△BCH,利用勾股定理和两点间的距离公式求得相关线段的长度,从而利用锐角三角函数的定义求得答案;
(3)如图2,过点D作DK⊥x轴于点K,构造直角△DOK,设D(x,x22x+3),则K(x,0).并由题意知点D位于第二象限.由于∠BAC是公共角,所以当△AOE与△ABC相似时,有2种情况:
①∠AOD=∠ABC.则tan∠AOD=tan∠ABC=3.由锐角三角函数定义列出比例式,从而求得点D的坐标.
②∠AOD=∠ACB.则tan∠AOD=tan∠ACB=2.由锐角三角函数定义列出比例式,从而求得点D的坐标.
(1)解:设抛物线的解析式为![]()
![]() 抛物线
抛物线![]() 过点
过点![]()

解得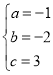
![]() 这条抛物线的解析式为
这条抛物线的解析式为![]()
顶点坐标为![]()
(2)解:过点![]() 作
作![]() ,垂足为
,垂足为![]()

![]()
![]()
![]()
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]()
![]()
![]()
![]()
(3)解:过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]()

设![]() ,则
,则![]() ,并由题意可得点
,并由题意可得点![]() 在第二象限
在第二象限
![]()
![]() 是公共角
是公共角
![]() 当
当![]() 与
与![]() 相似时
相似时
存在以下两种可能
①![]()
![]()
![]()
解得![]() ,
,![]() (舍去)
(舍去)

②![]()
![]()
![]()
解得![]() ,
,![]() (舍去)
(舍去)
![]()
综上所述:当![]() 与
与![]() 相似时,
相似时,
点![]() 的坐标为
的坐标为 或
或![]()


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN2,ND2,DH2之间的数量关系,并说明理由.
(3)在图①中,若EG=4,GF=6,求正方形ABCD的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
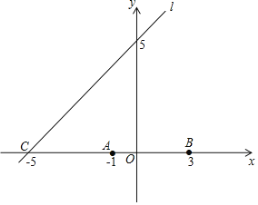
【题目】已知抛物线y=ax2+bx-3的图象与x轴交于点A(-1,0)和点B(3,0),顶点为D,点C是直线l:y=x+5与x轴的交点.
(1)求该二次函数的表达式;
(2)点E是直线l在第三象限上的点,连接EA、EB,当△ECA∽△BCE时,求E点的坐标;
(3)在(2)的条件下,连接AD、BD,在直线DE上是否存在点P,使得∠APD=∠ADB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:
如图,
(1)连接OP,作线段OP的垂直平分线MN交OP于点C;
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点;
(3)作直线PA,PB.所以直线PA,PB就是所求作的切线.
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是_____;由此可证明直线PA,PB都是⊙O的切线,其依据是_____.
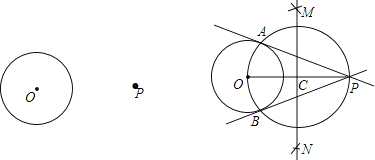
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,某小区2011年底拥有私家车125辆,2013年底私家车的拥有量达到180辆.
(1)若该小区2011年底到2014年底私家车拥有量的年平均增长率相同,则该小区到2014年底私家车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车位1 000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D是半圆AB的三等分点,过点C作AD延长线的垂线CE,垂足为E.

(1)求证:CE是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
(3)若弦CN过△ABC的内心点M,MN=![]() ,求CN.
,求CN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
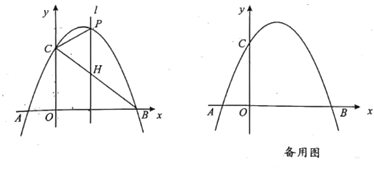
【题目】如图,已知抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0),与y轴交于点C。
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上一动点,过点P作x轴的垂线![]() ,交BC于点H.当点P运动到何处时满足PC=CH?求出此时点P的坐标;
,交BC于点H.当点P运动到何处时满足PC=CH?求出此时点P的坐标;
(3)若m≤x≤m+1时,二次函数y=ax2+bx+3的最大值为m,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com