
【题目】如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.
(1)上述三个条件中,哪两个条件 可判定△ABC是等腰三角形(用序号写出所有情形);
(2)选择第(1)小题中的一种情形,证明△ABC是等腰三角形.

【答案】(1) ①③或②③;(2)证明见解析.
【解析】试题分析:(1)①③;②③;①④;②④都可以组合证明△ABC是等腰三角形;(2)选①③为条件证明△ABC是等腰三角形,首先证明△EBO≌△DCO,可得BO=CO,根据等边对等角可得∠OBC=∠OCB,进而得到∠ABC=∠ACB,根据等角对等边可得AB=AC,即可得到△ABC是等腰三角形
试题解析:(1)①③;②③;①④;②④都可以组合证明△ABC是等腰三角形;(2)选①③为条件证明△ABC是等腰三角形;证明:∵在△EBO和△DCO中,∵∠EOB=∠DOC,∠EBO=∠DCO,EB=CD,∴△EBO≌△DCO(AAS),∴BO=CO,∴∠OBC=∠OCB,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,∴AB=AC,∴△ABC是等腰三角形.


科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧![]() 上.
上.
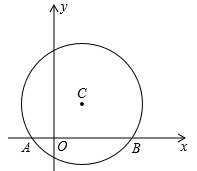
(1)求出A,B两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的集合内:+8.5,-3![]() ,0.3,0,-3.4,12,-9,4
,0.3,0,-3.4,12,-9,4![]() ,-1.2,-2.
,-1.2,-2.
(1)正数集合:{___________…};
(2)整数集合:{___________…};
(3)非正整数集合:{_____________…};
(4)负分数集合:{ ________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,过点A作⊙O的切线,交OC的延长线于点D,∠D=30°
(1)求∠B的度数;
(2)若OD⊥AB,BC=5,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系第一象限中,已知点A坐标为(1,0),点D坐标为(1,3),点G坐标为(1,1),动点E从点G出发,以每秒1个单位长度的速度匀速向点D方向运动,与此同时,x轴上动点B从点A出发,以相同的速度向右运动,两动点运动时间为t(0<t<2),以AD、AB分别为边作矩形ABCD,过点E作双曲线交线段BC于点F,作CD中点M,连接BE、EF、EM、FM.
(1)当t=1时,求点F的坐标.
(2)若BE平分∠AEF,则t的值为多少?
(3)若∠EMF为直角,则t的值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对当年初中升高中数学考试成绩进行抽样分析,试题满分100分,将所得成绩(均为整数)整理后,绘制了如图所示的统计图,根据图中所提供的信息,回答下列问题:

(1)共抽取了多少名学生的数学成绩进行分析?
(2)如果80分以上(包括80分)为优生,估计该年的优生率为多少?
(3)该年全市共有22000人参加初中升高中数学考试,请你估计及格(60分及60分以上)人数大约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两个直角顶点![]() 叠放在一起(如图①),其中
叠放在一起(如图①),其中![]() ,
,![]() ,
,![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)试猜想![]() 与
与![]() 的数量关系,请说明理由;
的数量关系,请说明理由;
(3)若按住三角板![]() 不动,绕顶点
不动,绕顶点![]() 转动三角板
转动三角板![]() ,试探究
,试探究![]() 等于多少度时,
等于多少度时,![]() ,并简要说明理由.
,并简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com