
【题目】某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)若某月用水12吨,应交水费多少元?
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,点A、C分别在y轴和x轴上,AB∥x轴,cosB=![]() .点P从B点出发,以1cm/s的速度沿边BA匀速运动,点Q从点A出发,沿线段AO-OC-CB匀速运动.点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△BPQ的面积为S(cm2), 已知S与t之间的函数关系如图(2)中的曲线段OE、线段EF与曲线段FG.
.点P从B点出发,以1cm/s的速度沿边BA匀速运动,点Q从点A出发,沿线段AO-OC-CB匀速运动.点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△BPQ的面积为S(cm2), 已知S与t之间的函数关系如图(2)中的曲线段OE、线段EF与曲线段FG.
(1)点Q的运动速度为 cm/s,点B的坐标为 ;
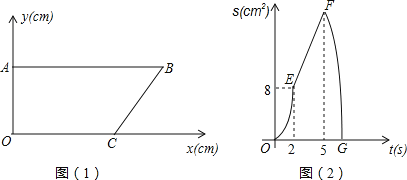
(2)求曲线FG段的函数解析式;
(3)当t为何值时,△BPQ的面积是四边形OABC的面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
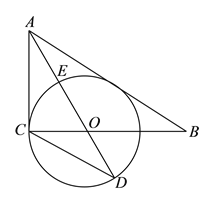
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的角平分线,以
的角平分线,以![]() 为圆心,
为圆心, ![]() 为半径作⊙
为半径作⊙![]() .
.
(![]() )求证:
)求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )已知
)已知![]() 交⊙
交⊙![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() ,
, ![]() ,求
,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的条件下,设⊙
)的条件下,设⊙![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.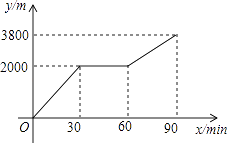
(1)小明行走的总路程是m,他途中休息了min.
(2)①当60≤x≤90时,求y与x的函数关系式;②当小丽到达缆车终点时,小明离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)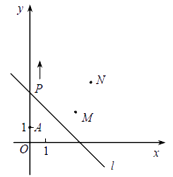
(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com