
【题目】如图,有三条格点线段AB、CD、DE(线段的端点是网格线的交点),它们组成的图形不是轴对称图形.现要通过平移或旋转,改变其中一条线段的位置,使运动后的这条线段与另两条线段组成一个轴对称图形.请分别填写三种平移方案和三种旋转方案平移方案:(移动方向限填“上”、“下”、“左”、“右”)
(1)将线段 向 平移1格;
(2)将线段 向 平移1格;
(3)将线段 向 平移1格;
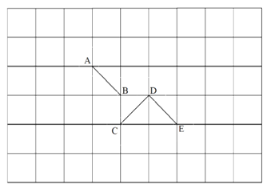
旋转方案:(限填绕A、B、C、D、E中的一点旋转且任意两条线段不重合)
(4)将线段 绕点 按 时针方向旋转 度;
(5)将线段 绕点 按 时针方向旋转 度;
(6)将线段 绕点 按 时针方向旋转 度;
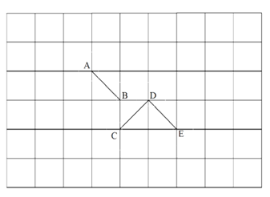
【答案】(1)![]() ,右;(2)
,右;(2)![]() ,下;(3)
,下;(3)![]() ,左; (4)将线段
,左; (4)将线段![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 度;(5)将线段
度;(5)将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 度;(6)将线段
度;(6)将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 度;
度;
【解析】
(1)根据平移的性质及轴对称的定义将AB向右平移1格即可;
(2)根据平移的性质及轴对称的定义将DE向下平移1格即可;
(3)根据平移的性质及轴对称的定义将DE向左平移1格即可;
(4)根据旋转的性质及轴对称的定义将线段![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 度即可;
度即可;
(5)根据旋转的性质及轴对称的定义将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 度即可;
度即可;
(6)根据旋转的性质及轴对称的定义将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 度即可;
度即可;
(1)将AB向右平移1格,运动后的这条AB线段与CD,DE线段组成一个轴对称图形;
故答案为:![]() ;右;
;右;
(2)将DE向下平移1格,运动后的这条DE线段与CD,AB线段组成一个轴对称图形;
故答案为:![]() ;下;
;下;
(3)将DE向左平移1格, 运动后的这条DE线段与CD,AB线段组成一个轴对称图形;
故答案为:![]() ;左;
;左;
(4)将线段![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 度, 运动后的这条CD线段与DE,AB线段组成一个轴对称图形;
度, 运动后的这条CD线段与DE,AB线段组成一个轴对称图形;
故答案为:将线段![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 度;
度;
(5)将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 度, 运动后的这条DE线段与CD,AB线段组成一个轴对称图形;
度, 运动后的这条DE线段与CD,AB线段组成一个轴对称图形;
故答案为:将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 度;
度;
(6)将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 度, 运动后的这条DE线段与CD,AB线段组成一个轴对称图形;
度, 运动后的这条DE线段与CD,AB线段组成一个轴对称图形;
故答案为:将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 度.
度.


科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分.而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的6位数密码就很有必要了.有一种用“因式分解法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:x3+2x2﹣x﹣2因式分解的结果为(x﹣1)(x+1)(x+2),当x=18时,x﹣1=17,x+1=19,x+2=20,此时可以得到数字密码171920.
(1)根据上述方法,当x=21,y=7时,对于多项式x3﹣xy2分解因式后可以形成哪些数字密码?(写出两个)
(2)若多项式x3+(m﹣3n)x2﹣nx﹣21因式分解后,利用本题的方法,当x=27时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 与X轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒).
与X轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒).

(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当![]() 时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,则最大正方形E的面积是_______.
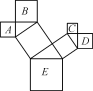
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的是_________(只填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
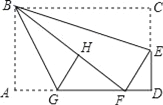
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是__.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
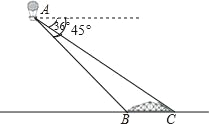
【题目】小明在热气球A上看到横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,36°.已知大桥BC与地面在同一水平面上,其长度为100m.请求出热气球离地面的高度(结果保留小数点后一位).参考数据:tan36°≈0.73.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司6天内货品进出仓库的吨数如下:(“+”表示进库,“-”表示出库)+31,-31,-16,+35,-38,-20
(1)经过这6天,仓库里的货品是______(填“增多了”或“减少了”)
(2)经过这6天,仓库管理员结算发现仓库还有货品460吨,那么6天前仓库里有货品多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少元装卸费?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com