
����Ŀ��һ���ı��α�һ���Խ��߷ָ�����������Σ�����ָ����õ��������������ƣ����ǾͰ������Խ��߳�Ϊ���ƶԽ���.
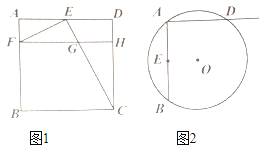
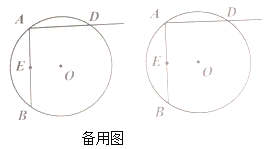
��1����ͼ��������![]() �ı߳�Ϊ4��
�ı߳�Ϊ4��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ���
�ϣ���![]() ���߶�
���߶�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����֤��
����֤��![]() Ϊ�ı���
Ϊ�ı���![]() �����ƶԽ��ߣ�
�����ƶԽ��ߣ�
��2�����ı���![]() �У�
�У�![]() ���ı���
���ı���![]() �����ƶԽ��ߣ�
�����ƶԽ��ߣ�![]() ��
��![]() ��
��![]() ����
����![]() �ij���
�ij���
��3����ͼ����֪�ı���![]() ��Բ
��Բ![]() ���ڽ��ı��Σ�
���ڽ��ı��Σ�![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ���е㣬��
���е㣬��![]() ������
������![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ���ı���
���ı���![]() �����ƶԽ��ߣ���ֱ��д���߶�
�����ƶԽ��ߣ���ֱ��д���߶�![]() �ij��ȣ�д��3�����ɣ�.
�ij��ȣ�д��3�����ɣ�.
���𰸡���1�������������2��![]() ��3����3���������.
��3����3���������.
��������
��1��ֻҪ֤����EAF�ס�FEG���ɽ�����⣻
��2����ͼ3�У���DE��BA��BA���ӳ�����E����AE=a����Rt��BDE�У����ù��ɶ��������������a�����������ι���������⼴�ɣ�
��3���ٵ���AFE�ס�EFCʱ������BC��AC��BD���ڵ���AFE�ס�FECʱ����CH��AD��AD���ӳ�����H����OM��AD��M������OA���۵���AFE�ס�CEFʱ���ֱ���⼴�ɣ�ע��𰸲�Ψһ��
�⣺��1����ͼ1����������![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �е�
�е�
��![]() ����
����![]() ����
����![]()
��![]()
��![]() ��
��![]()
��![]() �����ı���
�����ı���![]() Ϊƽ���ı���
Ϊƽ���ı���
��![]() ����
����![]() ��
��![]()
��![]()
��![]() Ϊ�ı���
Ϊ�ı���![]() �����ƶԽ���.
�����ƶԽ���.
��2����ͼ2������![]() ��
��![]() ������Ϊ
������Ϊ![]() ����
����![]()
��![]() ����
����![]() ����
����![]()
��![]() ��
��![]()
��![]()
![]() �������Ѿ���������
�������Ѿ���������
��![]()

�����������
����ͼ3����![]() ʱ��
ʱ��![]()
��![]() ����
����![]()

����ͼ4����![]() ʱ��
ʱ��![]()
��![]() ����
����![]()
���ϣ�![]() ��3
��3

��3������ͼ5���ߡ�FEC=��A=90������BEF=��BEC+��FEC=��A+��AEF��
��![]() ��
��![]() ����
����![]() ����
����![]()
����һ�����Ƚ�����![]() .
.

����ͼ������AFE�ס�FECʱ����CH��AD��AD���ӳ�����H����OM��AD��M������OA��

�ߡ�AFE�ס�FEC��
���AFE=��FEC��
��AD��EC��
���CEB=��DAB=90����
�ߡ�OMA=��AHC=90����
���ı���AEOM���ı���AECH���Ǿ��Σ�
��OM��AD��
��AM=MD=3��
��AM=OE=3��
��OE��AB��
��AE=EB=4��
��OA=![]() =5��
=5��
��CE=AH=8����AF=x����FH=8-x��CH=AE=4��
����AEF�ס�HFC���ɵ�![]() =
=![]() ��
��
��![]() ��
��
���x=4��
������x=4�Ƿ�ʽ���̵Ľ⣬
��AF=4��
����ͼ����AFE�ס�CEFʱ��֤�ı���AECF�Ǿ��Σ�AF=EC=8��
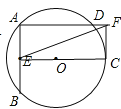
��������������������AF�ij�Ϊ![]() ��4��8�����𰸲�Ψһ��
��4��8�����𰸲�Ψһ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����Ե�OΪԲ�ĵİ�Բ�У�ABΪֱ������AB=4�����ð�Բ�۵���ʹ��A�͵�B���ڵ�O�����ۺ۷ֱ�ΪEC��FD����ͼ����Ӱ�������Ϊ��������

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
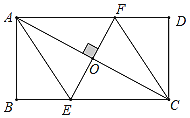
����Ŀ����ͼ������ABCD�ĶԽ���AC���е�ΪO������O��![]() ����BC���ڵ�E����AD���ڵ�F���ֱ�����AE��CF��
����BC���ڵ�E����AD���ڵ�F���ֱ�����AE��CF��
��1����֤���ı���AECF�����Σ�
��2����![]() ��
��![]() ����ֱ��д��EF�ij�Ϊ__________��
����ֱ��д��EF�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������ߣ�y����x��x��2����0��x��2����ΪC1������x�ύ�ڵ�O��A1����C1�Ƶ�A1��ת180����C2����x���ڵ�A2����C2�Ƶ�A2��ת180����C3����x���ڵ�A3����˽�����ȥ����C2019�Ķ���������_____��
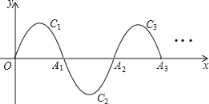
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������L��y����x2+bx+c��������ԭ�㣬�����ĶԳ���ֱ��x��2����A�㣮
��1��ֱ��д�������ߵĽ���ʽ��
��2����A��x�����У���y����B��C�㣬��������L�ĶԳ�����D�㣬��������ֱ��y��kx��2k+8��k��0����������L����M��N�㣬��AMN���������2������
�ٻ�BC�ij���
��k��ֵ��
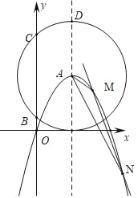
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ�˶�����ֱ��������б���ϵ����ߵ���б�ߵ�һ����֮����������˼����
��1������Ϊ�ö������涨�����������һ��������ij�����ϵ����ߵ��ڸñ߳���һ�룬��ô�����������ֱ����������Ӧ�ó��������ܰ�С��֤��һ������ͼ�٣�����ABC�У�AD��BC���ϵ����ߣ���AD��BD��CD����֤����BAC��90����
��2����������С��������һ�����⣺��ͼ�ڣ���֪����ABCD������ھ��������һ��E��ʹ��AE��CE����֤��BE��DE����������֤��������ֱ���õ��ڣ�1���ʵĽ��ۣ�
��3���ڵڣ�2���ʵ������£������AEDǡ���ǵȱ������Σ�ֱ���õ�ʽ��ʾ����ʱ���ε������ڱ�AB��BC��������ϵ��
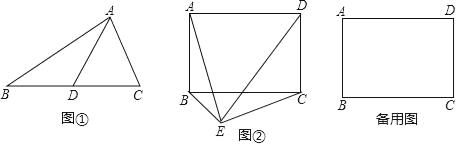
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��Բ��P(m��n)��������y��![]() �ϣ�
�ϣ�
(1)д��m��n֮��Ĺ�ϵʽ��
(2)����P���������ᶼ����ʱ�������P�İ뾶��
(3)����P�İ뾶��8��������x���Ͻصõ���MN������0��MN��2![]() ʱ�����m��n�ķ�Χ��
ʱ�����m��n�ķ�Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��ax+b��a��0����ͼ���뷴��������y��![]() ��k��0����ͼ���ཻ��A��B�����ҵ�A������Ϊ��3��1������B�����꣨��1��n����
��k��0����ͼ���ཻ��A��B�����ҵ�A������Ϊ��3��1������B�����꣨��1��n����
��1���ֱ������������Ľ���ʽ��
��2������AOB�������
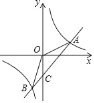
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
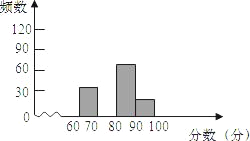
����Ŀ��ijУ�����ֹ�����������������������ͬѧ�ijɼ�����������ͼ�����£�
������ | Ƶ�� | Ƶ�� |
60��x��70 | 30 | 0.15 |
70��x��80 | m | 0.45 |
80��x��90 | 60 | n |
90��x��100 | 20 | 0.1 |
���������ͼ���ṩ����Ϣ������������⣺
��1������m��n����ʾ�����ֱ�Ϊ��m��______��n��______��
��2������ͼ�У���ȫƵ���ֲ�ֱ��ͼ��
��3�������ɼ�����λ�������ĸ������Σ�
��4����������ɼ�80�����ϣ���80�֣����Ի�ý�������ô�����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com