
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
云端服务器数量 (台) (台) | 32 | 34 | 36 | 38 | 40 | 42 | 44 |
 (台)与月份x(月)之间存在如图所示的变化趋势:
(台)与月份x(月)之间存在如图所示的变化趋势:
 与x之间的函数关系式,根据如图所示的变化趋势,直接写出
与x之间的函数关系式,根据如图所示的变化趋势,直接写出 与x之间满足的一次函数关系式;
与x之间满足的一次函数关系式; (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式:  ,(1≤x≤7,且x为整数);8至12月份的资金投入
,(1≤x≤7,且x为整数);8至12月份的资金投入 (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式: (8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;
(8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;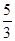 ,a=-1.5,在对称轴的右侧W2随着x的增大而减小.
,a=-1.5,在对称轴的右侧W2随着x的增大而减小.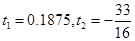 (舍去)..
(舍去)..

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源:不详 题型:解答题
 经过点B(
经过点B( ,2),且与x轴交于点A.将抛物线
,2),且与x轴交于点A.将抛物线 沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
 平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,下列说法错误的是( )
,下列说法错误的是( )A.当 时, 时, 随 随 的增大而减小 的增大而减小 |
B.若图象与 轴有交点,则 轴有交点,则 |
C.当 时,不等式 时,不等式 的解集是 的解集是 |
D.若将图象向上平移1个单位,再向左平移3个单位后过点 ,则 ,则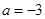 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 图像中,观察得出了下面的五条信息:①
图像中,观察得出了下面的五条信息:① ,②
,② ,③函数的最小值为-3,④当
,③函数的最小值为-3,④当 时,
时, ,⑤当
,⑤当 ,
, 。你认为其中正确的个数为
。你认为其中正确的个数为
| A.2 | B.3 | C.4 | D.5 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且
与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.a>0,b<0,c>0 | B. a<0,b<0,c>0 |
| C.a<0,b>0,c<0 | D. a<0,b>0,c>0 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
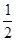 ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 间,当每间客房的定价为每天
间,当每间客房的定价为每天 元时,客房会全部住满.当每间客房每天的定价每涨
元时,客房会全部住满.当每间客房每天的定价每涨 元时,就会有
元时,就会有 间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出
间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出 元的各种费用.
元的各种费用. (元)与每间客房涨价
(元)与每间客房涨价 (元)之间的函数关系式;
(元)之间的函数关系式; 元,
元, 元的利润是否为该天的最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时客房定价应为多少元?
元的利润是否为该天的最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时客房定价应为多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com