
ЁОЬтФПЁПФГЩЬГЁЯњЪлУПИіНјМлЮЊ150дЊКЭ120дЊЕФAЁЂBСНжжаЭКХЕФзуЧђЃЌШчБэЪЧНќСНжмЕФЯњЪлЧщПіЃК
ЯњЪлЪБЖЮ | ЯњЪлЪ§СП | ЯњЪлЪеШы | |
AжжаЭКХ | BжжаЭКХ | ||
ЕквЛжм | 3Иі | 4Иі | 1200дЊ |
ЕкЖўжм | 5Иі | 3Иі | 1450дЊ |
![]() НјМлЁЂЪлМлОљБЃГжВЛБфЃЌРћШѓ
НјМлЁЂЪлМлОљБЃГжВЛБфЃЌРћШѓ![]() ЯњЪлЪеШы
ЯњЪлЪеШы![]() НјЛѕГЩБО
НјЛѕГЩБО![]()
(1)ЧѓAЁЂBСНжжаЭКХЕФзуЧђЕФЯњЪлЕЅМлЃЛ
(2)ШєЩЬГЁзМБИгУВЛЖргк8400дЊЕФН№ЖюдйЙКНјетСНжжаЭКХЕФзуЧђЙВ60ИіЃЌЧѓAжжаЭКХЕФзуЧђзюЖрФмВЩЙКЖрЩйИіЃП
(3)дк![]() ЕФЬѕМўЯТЃЌЩЬГЁЯњЪлЭъет60ИізуЧђФмЗёЪЕЯжРћШѓГЌЙ§2550дЊЃЌШєФмЃЌЧыИјГіЯргІЕФВЩЙКЗНАИЃЛШєВЛФмЧыЫЕУїРэгЩЃЎ
ЕФЬѕМўЯТЃЌЩЬГЁЯњЪлЭъет60ИізуЧђФмЗёЪЕЯжРћШѓГЌЙ§2550дЊЃЌШєФмЃЌЧыИјГіЯргІЕФВЩЙКЗНАИЃЛШєВЛФмЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉAаЭКХзуЧђЕЅМлЪЧ200дЊЃЌBаЭКХзуЧђЕЅМлЪЧ150дЊЃЎЃЈ2ЃЉ40ИіЃЎЃЈ3ЃЉга3жжВЩЙКЗНАИЃЎЗНАИвЛЃКAаЭКХ38ИіЃЌBаЭКХ22ИіЃЛЗНАИЖўЃКAаЭКХ39ИіЃЌBаЭКХ21ИіЃЛЗНАИШ§ЃКAаЭКХ40ИіЃЌBаЭКХ20ИіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩш![]() ЁЂ
ЁЂ![]() СНжжаЭКХЕФзуЧђЯњЪлЕЅМлЗжБ№ЪЧ
СНжжаЭКХЕФзуЧђЯњЪлЕЅМлЗжБ№ЪЧ![]() дЊКЭ
дЊКЭ![]() дЊЃЌИљОн
дЊЃЌИљОн![]() Иі
Иі![]() аЭКХКЭ
аЭКХКЭ![]() Иі
Иі![]() аЭКХЕФзуЧђЪеШы
аЭКХЕФзуЧђЪеШы![]() дЊЃЌ
дЊЃЌ![]() Иі
Иі![]() аЭКХКЭ
аЭКХКЭ![]() Иі
Иі![]() аЭКХЕФЕчЩШЪеШы
аЭКХЕФЕчЩШЪеШы![]() дЊЃЌСаЗНГЬзщЧѓНтЃЛ
дЊЃЌСаЗНГЬзщЧѓНтЃЛ
ЃЈ2ЃЉЩш![]() аЭКХзуЧђЙКНј
аЭКХзуЧђЙКНј![]() ИіЃЌ
ИіЃЌ![]() аЭКХзуЧђЙКНј
аЭКХзуЧђЙКНј![]() ИіЃЌИљОнН№ЖюВЛЖргр
ИіЃЌИљОнН№ЖюВЛЖргр![]() дЊЃЌСаВЛЕШЪНЧѓНтЃЛ
дЊЃЌСаВЛЕШЪНЧѓНтЃЛ
ЃЈ3ЃЉИљОн![]() аЭКХзуЧђЕФНјМлКЭЪлМлЃЌ
аЭКХзуЧђЕФНјМлКЭЪлМлЃЌ![]() аЭКХзуЧђЕФНјМлКЭЪлМлвдМАзмРћШѓ=вЛИіРћШѓЁСзмЪ§ЃЌСаГіВЛЕШЪНЃЌЧѓГі
аЭКХзуЧђЕФНјМлКЭЪлМлвдМАзмРћШѓ=вЛИіРћШѓЁСзмЪ§ЃЌСаГіВЛЕШЪНЃЌЧѓГі![]() ЕФжЕЃЌдйИљОн
ЕФжЕЃЌдйИљОн![]() ЮЊећЪ§ЃЌМДПЩЕУГіД№АИ.
ЮЊећЪ§ЃЌМДПЩЕУГіД№АИ.
![]() НтЃКЩшAЁЂBСНжжаЭКХЕФзуЧђЯњЪлЕЅМлЗжБ№ЪЧxдЊКЭyдЊЃЌСаГіЗНГЬзщЃК
НтЃКЩшAЁЂBСНжжаЭКХЕФзуЧђЯњЪлЕЅМлЗжБ№ЪЧxдЊКЭyдЊЃЌСаГіЗНГЬзщЃК![]()
НтЕУ![]()
AаЭКХЧђЕЅМлЪЧ200дЊЃЌBаЭКХзуЧђЕЅМлЪЧ150дЊЃЎ
![]() НтЃКЩшAаЭКХзуЧђЙКНјaИіЃЌBаЭКХзуЧђЙКНј
НтЃКЩшAаЭКХзуЧђЙКНјaИіЃЌBаЭКХзуЧђЙКНј![]() ИіЃЌИљОнЬтвтЕУЃК
ИіЃЌИљОнЬтвтЕУЃК
![]()
НтЕУ![]() ЃЌЫљвдAаЭКХзуЧђзюЖрФмВЩЙК40ИіЃЎ
ЃЌЫљвдAаЭКХзуЧђзюЖрФмВЩЙК40ИіЃЎ
![]() НтЃКШєРћШѓГЌЙ§2550дЊЃЌаы
НтЃКШєРћШѓГЌЙ§2550дЊЃЌаы![]()
![]() ЃЌвђЮЊaЮЊећЪ§ЃЌ
ЃЌвђЮЊaЮЊећЪ§ЃЌ
Ыљвд![]()
ФмЪЕЯжРћШѓГЌЙ§2550дЊЃЌга3жжВЩЙКЗНАИЃЎ
ЗНАИвЛЃКAаЭКХ38ИіЃЌBаЭКХ22ИіЃЛ
ЗНАИЖўЃКAаЭКХ39ИіЃЌBаЭКХ21ИіЃЛ
ЗНАИШ§ЃКAаЭКХ40ИіЃЌBаЭКХ20ИіЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§yЃНkxЃЋbЕФЭМЯѓОЙ§A(Ѓ2,Ѓ1)ЃЌB(1ЃЌ3)СНЕуЃЌВЂЧвНЛxжсгкЕуCЃЌНЛyжсгкЕуD.

ЃЈ1ЃЉЧѓИУвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЕуCКЭЕуDЕФзјБъЃЛ
ЃЈ3ЃЉЧѓЁїAOBЕФУцЛ§ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЪЧзјБъдЕуЃЌЕуAдкyжсЕФе§АыжсЩЯЃЌзјБъЮЊ![]() ЃЌЕуBдкxжсЕФИКАыжсЩЯЃЌзјБъЮЊ
ЃЌЕуBдкxжсЕФИКАыжсЩЯЃЌзјБъЮЊ![]() ЃЌЭЌЪБ
ЃЌЭЌЪБ![]() Тњзу
Тњзу![]() ЃЌСЌНгABЃЌЧвAB=10ЃЎЕуDЪЧxжсе§АыжсЩЯЕФвЛИіЖЏЕуЃЌЕуEЪЧЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЌСЌНгDEЃЎ
ЃЌСЌНгABЃЌЧвAB=10ЃЎЕуDЪЧxжсе§АыжсЩЯЕФвЛИіЖЏЕуЃЌЕуEЪЧЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЌСЌНгDEЃЎ

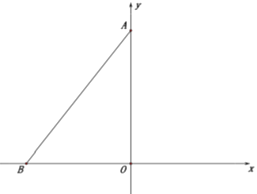
ЃЈ1ЃЉЧѓAЁЂBСНЕузјБъЃЛ
ЃЈ2ЃЉШє![]() ЃЌЕуDЕФКсзјБъЮЊxЃЌЯпЖЮ
ЃЌЕуDЕФКсзјБъЮЊxЃЌЯпЖЮ![]() ЕФГЄЮЊdЃЌЧыгУКЌxЕФЪНзгБэЪОdЃЛ
ЕФГЄЮЊdЃЌЧыгУКЌxЕФЪНзгБэЪОdЃЛ
ЃЈ3ЃЉШє![]() ЃЌAFЁЂDFЗжБ№ЦНЗжЁЯBAOЁЂЁЯBDEЃЌЯрНЛгкЕуFЃЌЧѓЁЯFЕФЖШЪ§ЃЎ
ЃЌAFЁЂDFЗжБ№ЦНЗжЁЯBAOЁЂЁЯBDEЃЌЯрНЛгкЕуFЃЌЧѓЁЯFЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавЛжБНЧШ§НЧаЮжНЦЌЃЌЁЯCЃН90ЁуЃЌBCЃН6ЃЌACЃН8ЃЌЯжНЋЁїABCАДШчЭМФЧбљелЕўЃЌЪЙЕуAгыЕуBжиКЯЃЌелКлЮЊDEЃЌдђCEЕФГЄЮЊЃЈЁЁЁЁЃЉ
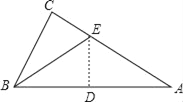
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
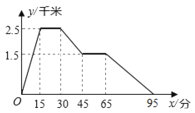
ЁОЬтФПЁПШчЭМЫљЪОЃКЭМЯѓжаЫљЗДгГЕФЙ§ГЬЪЧЃКаЁЖЌДгМвХмВНШЅЬхг§ГЁЃЌдкФЧРяЖЭСЖСЫвЛеѓКѓЃЌгжШЅдчВЭЕъГддчВЭЃЌШЛКѓЩЂВНзпЛиМвЃЎЦфжаxжсБэЪОЪБМфЃЌyжсБэЪОаЁЖЌРыМвЕФОрРыЃЎИљОнЭМЯѓЬсЙЉЕФаХЯЂЃЌЯТСаЫЕЗЈе§ШЗЕФга________.
ЂйЃЎЬхг§ГЁРыаЁЖЌМв2.5ЧЇУз ЂкЃЎаЁЖЌдкЬхг§ГЁЖЭСЖСЫ15Зжжг
ЂлЃЎЬхг§ГЁРыдчВЭЕъ4ЧЇУз ЂмЃЎаЁЖЌДгдчВЭЕъЛиМвЕФЦНОљЫйЖШЪЧ3ЧЇУз/аЁЪБ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+cОЙ§AЃЈ1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3ЃЉШ§ЕуЃЎ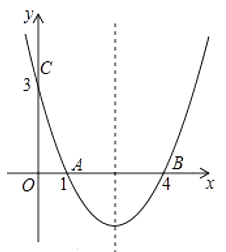
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЫФБпаЮPAOCЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіЫФБпаЮPAOCжмГЄЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМЂкЃЌЕуQЪЧЯпЖЮOBЩЯвЛЖЏЕуЃЌСЌНгBCЃЌдкЯпЖЮBCЩЯЪЧЗёДцдкетбљЕФЕуMЃЌЪЙЁїCQMЮЊЕШбќШ§НЧаЮЧвЁїBQMЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2018Фъ1дТ20ШеЃЌЩНЮїгРДСЫЁАИДаЫКХЁБСаГЕЃЌгыЁАКЭаГКХЁБЯрБШЃЌЁАИДаЫКХЁБСаГЕЪБЫйИќПьЃЌАВШЋадИќКУЃЎвбжЊЁАЬЋдФЯЉББОЉЮїЁБШЋГЬДѓдМ500ЧЇУзЃЌЁАИДаЫКХЁБG92ДЮСаГЕЦНОљУПаЁЪББШФГСаЁАКЭаГКХЁБСаГЕЖрааЪЛ40ЧЇУзЃЌЦфааЪЛЪБМфЪЧИУСаЁАКЭаГКХЁБСаГЕааЪЛЪБМфЕФ![]() ЃЈСНСаГЕжаЭОЭЃСєЪБМфОљГ§ЭтЃЉЃЎОВщбЏЃЌЁАИДаЫКХЁБG92ДЮСаГЕДгЬЋдФЯЕНББОЉЮїЃЌжаЭОжЛгаЪЏМвзЏвЛеОЃЌЭЃСє10ЗжжгЃЎЧѓГЫзјЁАИДаЫКХЁБG92ДЮСаГЕДгЬЋдФЯЕНББОЉЮїашвЊЖрГЄЪБМфЃЎ
ЃЈСНСаГЕжаЭОЭЃСєЪБМфОљГ§ЭтЃЉЃЎОВщбЏЃЌЁАИДаЫКХЁБG92ДЮСаГЕДгЬЋдФЯЕНББОЉЮїЃЌжаЭОжЛгаЪЏМвзЏвЛеОЃЌЭЃСє10ЗжжгЃЎЧѓГЫзјЁАИДаЫКХЁБG92ДЮСаГЕДгЬЋдФЯЕНББОЉЮїашвЊЖрГЄЪБМфЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЌBЕФзјБъЗжБ№ЮЊ(Ѓ1ЃЌ0)ЃЌ(3ЃЌ0)ЃЌЯжЭЌЪБНЋЕуAЃЌBЗжБ№ЯђЩЯЦНвЦ2ИіЕЅЮЛГЄЖШЃЌдйЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНAЃЌBЕФЖдгІЕуCЃЌDЃЌСЌНгACЃЌBDЃЌCD.
(1)жБНгаДГіЕуCЃЌDЕФзјБъЃЌЧѓГіЫФБпаЮABDCЕФУцЛ§ЃЛ
(2)дкxжсЩЯЪЧЗёДцдквЛЕуFЃЌЪЙЕУШ§НЧаЮDFCЕФУцЛ§ЪЧШ§НЧаЮDFBУцЛ§ЕФ2БЖЃЌШєДцдкЃЌЧыЧѓГіЕуFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЯжАДШчЯТВНжшзїЭМЃК
ЂйЗжБ№вдAЃЌCЮЊдВаФЃЌaЮЊАыОЖЃЈaЃО![]() ACЃЉзїЛЁЃЌСНЛЁЗжБ№НЛгкMЃЌNСНЕуЃЛ
ACЃЉзїЛЁЃЌСНЛЁЗжБ№НЛгкMЃЌNСНЕуЃЛ
ЂкЙ§MЃЌNСНЕузїжБЯпMNНЛABгкЕуDЃЌНЛACгкЕуEЃЛ
ЂлНЋЁїADEШЦЕуEЫГЪБеыа§зЊ180ЁуЃЌЩшЕуDЕФЯёЮЊЕуFЃЎ

ЃЈ1ЃЉЧыдкЭМжажБЯпБъГіЕуFВЂСЌНгCFЃЛ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮBCFDЪЧЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉЕБЁЯBЮЊЖрЩйЖШЪБЃЌЫФБпаЮBCFDЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com