
 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).分析 (1)利用网格特点和旋转的性质画出A、B、C的对应点A1、B1、C1,从而得到△A1B1C1,然后写出A的对应点A1的坐标;
(2)由于点A所走过的路线是以点O为圆心,OA为半径,圆心角为90°所对的弧,然后根据弧长公式求解.
解答 解:(1)如图,△A1B1C1为所作,A的对应点A1的坐标为(2,1);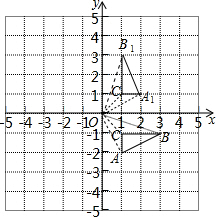
(2)OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
所以点A所走过的路线长=$\frac{90•π•\sqrt{5}}{180}$=$\frac{\sqrt{5}}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
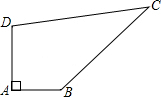 如图,某开发区计划在一块四边形的空地ABCD上种植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,种植每平方米草皮的预算费用为300元,若第一年对草坪的保养费用占种植草皮总预算的4%,以后每年的保养费用都将在前一年的基础上递增2%,求第三年的草坪保养费用.
如图,某开发区计划在一块四边形的空地ABCD上种植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,种植每平方米草皮的预算费用为300元,若第一年对草坪的保养费用占种植草皮总预算的4%,以后每年的保养费用都将在前一年的基础上递增2%,求第三年的草坪保养费用.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
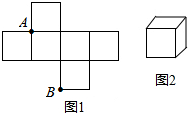 如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,一个蚂蚁在图1中的A点,围成图2后,蚂蚁从A点开始沿正方体的棱爬行,求爬到B点的最短距离是多少?
如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,一个蚂蚁在图1中的A点,围成图2后,蚂蚁从A点开始沿正方体的棱爬行,求爬到B点的最短距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
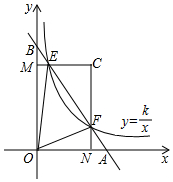 如图,平面坐标系中,AB交矩形ONCM于E、F,若$\frac{BE}{BF}$=$\frac{1}{m}$(m>1),且双曲线y=$\frac{k}{x}$也过E、F两点,记S△CEF=S1,S△OEF=S2,用含m的代数式表示$\frac{{s}_{1}}{{s}_{2}}$.
如图,平面坐标系中,AB交矩形ONCM于E、F,若$\frac{BE}{BF}$=$\frac{1}{m}$(m>1),且双曲线y=$\frac{k}{x}$也过E、F两点,记S△CEF=S1,S△OEF=S2,用含m的代数式表示$\frac{{s}_{1}}{{s}_{2}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com