
【题目】如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
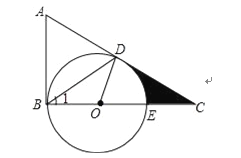
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
【答案】(1)AC是⊙O的切线;(2)![]()
【解析】
试题分析:(1)由OD=OB得∠1=∠ODB,则根据三角形外角性质得∠DOC=∠1+∠ODB=2∠1,而∠A=2∠1,所以∠DOC=∠A,由于∠A+∠C=90°,所以∠DOC+∠C=90°,则可根据切线的判定定理得到AC是⊙O的切线;
(2)由∠A=60°得到∠C=30°,∠DOC=60°,根据含30度的直角三角形三边的关系得CD=2![]() ,然后利用阴影部分的面积=S△COD﹣S扇形DOE和扇形的面积公式求解.
,然后利用阴影部分的面积=S△COD﹣S扇形DOE和扇形的面积公式求解.
试题解析:(1)证明:∵OD=OB,
∴∠1=∠ODB,
∴∠DOC=∠1+∠ODB=2∠1,
∵∠A=2∠1,
∴∠DOC=∠A,
∵∠A+∠C=90°,
∴∠DOC+∠C=90°,
∴OD⊥DC,
∴AC是⊙O的切线;
(2)解:∵∠A=60°,
∴∠C=30°,∠DOC=60°,
在Rt△DOC中,OD=2,
∴CD=![]() OD=2
OD=2![]() ,
,
∴阴影部分的面积=S△COD﹣S扇形DOE
=![]() ×2×2
×2×2![]() ﹣
﹣![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x﹣3,下列判断正确的是( )
A. 开口方向向上,y有最小值是﹣2 B. 抛物线与x轴有两个交点
C. 顶点坐标是(﹣1,﹣2) D. 当x<1时,y随x增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
①过两点有且只有一条直线; ②两直线相交只有一个交点;
③0的绝对值是它本身 ④射线AB和射线BA是同一条射线.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,若平移二次函数y=(x﹣6)(x﹣7)﹣3的图象,使其与x轴交于两点,且此两点的距离为1个单位,则平移方式为( )
A. 向左平移3个单位 B. 向右平移3个单位
C. 向上平移3个单位 D. 向下平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视,正在播放《新闻联播》”是必然事件
B. 一组数据的波动越大,方差越小
C. 数据1,1,2,2,3的众数是3
D. 想了解某种饮料中含色素的情况,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列的推理过程补充完整,并在括号里填上推理的依据:
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.
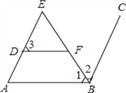
试说明:DF∥AB
解:因为BE是∠ABC的角平分线
所以 (角平分线的定义)
又因为∠E=∠1(已知)
所以∠E=∠2( )
所以 ( )
所以∠A+∠ABC=180°( )
又因为∠3+∠ABC=180°(已知)
所以 ( )
所以DF∥AB( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com