
【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起. 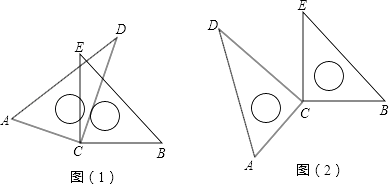
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
【答案】
(1)解:∠ACE=∠BCD,理由如下:
∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,
∴∠ACE=∠BCD
(2)解:若∠DCE=30°,∠ACD=90°,
∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,
∵∠BCE=90°且∠ACB=∠ACE+∠BCE,
∠ACB=90°+60°=150°
(3)解:猜想∠ACB+∠DCE=180°.理由如下:
∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°
(4)解:成立
【解析】(1)根据余角的性质,可得答案;(2)根据余角的定义,可得∠ACE,根据角的和差,可得答案;(3)根据角的和差,可得答案;(4)根据角的和差,可得答案.
【考点精析】关于本题考查的余角和补角的特征,需要了解互余、互补是指两个角的数量关系,与两个角的位置无关才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,C为射线AB上一点,AB=30,AC比BC的 ![]() 多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: ①BC=2AC;②AB=4NQ;③当PB=
多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: ①BC=2AC;②AB=4NQ;③当PB= ![]() BQ时,t=12,其中正确结论的个数是( )
BQ时,t=12,其中正确结论的个数是( )![]()
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
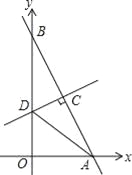
【题目】如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x﹣4)+8(4﹣x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.
(1)求线段AB的长;
(2)求tan∠DAO的值;
(3)若把△ADC绕点A顺时针旋转α°(0<α<90),点D,C的对应点分别为D1,C1,得到△AD1C1,当AC1∥y轴时,分别求出点C1,点D1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD. 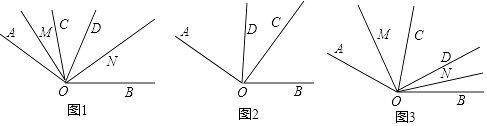
(1)若∠COD=180°﹣α时,探索下面两个问题: ①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)如图3,当∠COD=kα,且OC在OD左侧时,直接写出∠MON的度数(用含α、k的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com