
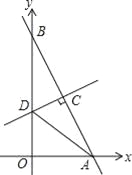
【题目】如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x﹣4)+8(4﹣x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.
(1)求线段AB的长;
(2)求tan∠DAO的值;
(3)若把△ADC绕点A顺时针旋转α°(0<α<90),点D,C的对应点分别为D1,C1,得到△AD1C1,当AC1∥y轴时,分别求出点C1,点D1的坐标.
【答案】(1)、4![]() ;(2)、
;(2)、![]() ;(3)、C1(4,2
;(3)、C1(4,2![]() ),D1(4-
),D1(4-![]() ,2
,2![]() )
)
【解析】试题分析:(1)先根据方程的解求得线段OA,OB的长,再根据勾股定理求得AB的长;(2)先根据线段垂直平分线的性质,得到AD=BD,再根据Rt△AOD中的勾股定理,求得OD的长,并计算tan∠DAO的值;(3)先根据旋转的性质,求得AC1和C1D1的长,再根据OA=4,AC1∥y轴,求得点C1和点D1的坐标.
试题解析:(1)由方程x(x﹣4)+8(4﹣x)=0,解得
x1=4,x2=8,
即OA=4,OB=8,
∴由勾股定理可得AB=![]()
(2)∵CD为AB的垂直平分线,
∴AD=BD
∵在Rt△AOD中,OD2+OA2=AD2
即OD2+42=(8﹣OD)2,
∴OD=3
∴![]()
(3)由旋转可得,AC1=AC=2![]() ,C1D1=CD=
,C1D1=CD=![]() =
=![]()
又∵OA=4,AC1∥y轴
∴C1(4,2![]() ),D1(4-
),D1(4-![]() ,2
,2![]() )
)


科目:初中数学 来源: 题型:
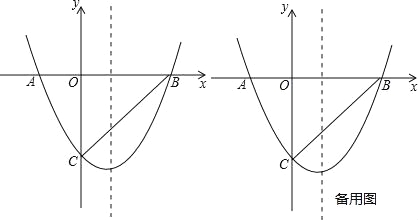
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣2,0)和点B(4,0),与y轴交于点C(0,﹣4).
(1)求二次函数的解析式,并写出抛物线的对称轴,顶点坐标;
(2)设E时抛物线对称轴上一点,当∠BEC=90°时,求点E的坐标;
(3)若P(m,n)是抛物线上一个动点(其中m>0,n<0),是否存在这样的点P,使得△PBC的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
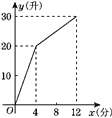
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.那么,从关闭进水管起________分钟该容器内的水恰好放完.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起. 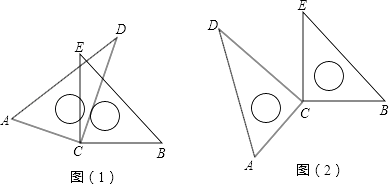
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
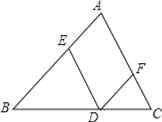
【题目】已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.
(1)证明:△BDE∽△DCF;
(2)若△ABC的面积为10,点G为线段AF上的任意一点,设FC:AC=n,△DEG的面积为S,求S关于n的关系式,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于6.3×103与6300这两个近似数,下列说法中,正确的是( ).
A.它们的有效数字与精确位数都不相同
B.它们的有效数字与精确位数都相同
C.它们的精确位数不相同,有效数字相同
D.它们的有效数字不相同,精确位数相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某新型感冒病毒的直径约为0.000 000 733米,将0.000 000 733用科学记数法表示为( )
A. 7.33×10-6B. 7.33×10-7C. 7.33×106D. 7.33×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com