
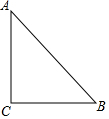 如图,Rt△ABC中,∠C=90°,AC=BC=5,若P为平面内一点,且AP=$\sqrt{10}$,BP=2$\sqrt{5}$,则CP=5或$\sqrt{5}$.
如图,Rt△ABC中,∠C=90°,AC=BC=5,若P为平面内一点,且AP=$\sqrt{10}$,BP=2$\sqrt{5}$,则CP=5或$\sqrt{5}$. 分析 如图作PE⊥AC于E,PF⊥BC于F.设PE=a,PF=b.利用勾股定理列出方程即可解决问题.
解答 解:如图作PE⊥AC于E,PF⊥BC于F.设PE=a,PF=b.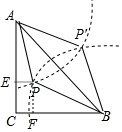
则有$\left\{\begin{array}{l}{(5-a)^{2}+{b}^{2}=10}\\{{a}^{2}+(5-b)^{2}=20}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$或$\left\{\begin{array}{l}{a=4}\\{b=3}\end{array}\right.$,
当a=2,b=1时,点P在△ABC内,
∴PC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
当a=4,b=3时,点P在△ABC内,
∴PC=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故答案为$\sqrt{5}$或5.
点评 本题考查勾股定理、二元二次方程组等知识,解题的关键是学会利用参数构建方程组解决问题,属于中考常考题型.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
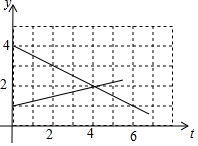 某工厂有甲、乙两个长方体的水池,甲水池较深,甲池的水用抽水机匀速地抽入乙池,如图所示的是甲、乙两个水池水的深度y(m)与抽水时间t(h)的函数关系的图象.
某工厂有甲、乙两个长方体的水池,甲水池较深,甲池的水用抽水机匀速地抽入乙池,如图所示的是甲、乙两个水池水的深度y(m)与抽水时间t(h)的函数关系的图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
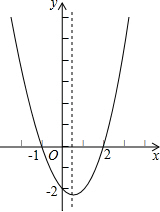 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当-1<x<2时,y<0 | D. | 当x>$\frac{1}{3}$时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.
如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
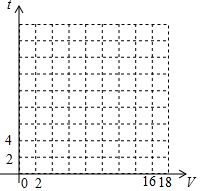 某一蓄水池中有水若干吨,若单一个 出水口,排水速度v(m3/h)与排完水池中的水所用的时间之间t(h)的一组对应值如下表:
某一蓄水池中有水若干吨,若单一个 出水口,排水速度v(m3/h)与排完水池中的水所用的时间之间t(h)的一组对应值如下表:| 排水速度 (m3/h) | 1 | 2 | 3 | 4 | 6 | 8 | 12 |
| 所用的时间 t(h) | 12 | 6 | 4 | 3 | 2 | 1.5 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
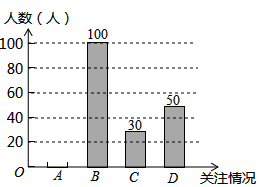 温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:
温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:| 关注情况 | 频数 | 频率 |
| A.高度关注 | m | 0.1 |
| B.一般关注 | 100 | 0.5 |
| C.不关注 | 30 | n |
| D.不知道 | 50 | 0.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com