
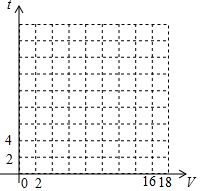
 某一蓄水池中有水若干吨,若单一个 出水口,排水速度v(m3/h)与排完水池中的水所用的时间之间t(h)的一组对应值如下表:
某一蓄水池中有水若干吨,若单一个 出水口,排水速度v(m3/h)与排完水池中的水所用的时间之间t(h)的一组对应值如下表:| 排水速度 (m3/h) | 1 | 2 | 3 | 4 | 6 | 8 | 12 |
| 所用的时间 t(h) | 12 | 6 | 4 | 3 | 2 | 1.5 | 1 |
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
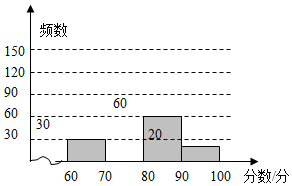 为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | m | 0.45 |
| 80≤x<90 | 60 | n |
| 90≤x≤100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 3 | -2 | -5 | -6 | -5 | … |
| A. | 抛物线开口向下 | |
| B. | 抛物线与y轴交于正半轴 | |
| C. | 方程ax2+bx+c=0的正根在1与2之间 | |
| D. | 当x=-3时的函数值比x=1.5时的函数值大 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
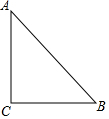 如图,Rt△ABC中,∠C=90°,AC=BC=5,若P为平面内一点,且AP=$\sqrt{10}$,BP=2$\sqrt{5}$,则CP=5或$\sqrt{5}$.
如图,Rt△ABC中,∠C=90°,AC=BC=5,若P为平面内一点,且AP=$\sqrt{10}$,BP=2$\sqrt{5}$,则CP=5或$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,分别表示甲步行与乙汽自行车(在同一条路上)行走的路程S甲、S乙与时间t的关系,观察图象并回答下列问题:
如图,分别表示甲步行与乙汽自行车(在同一条路上)行走的路程S甲、S乙与时间t的关系,观察图象并回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
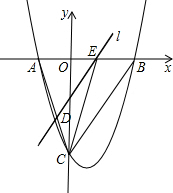 如图,抛物线y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4与x轴交于A,B两点,与y轴交于点C,连接BC,AC.
如图,抛物线y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4与x轴交于A,B两点,与y轴交于点C,连接BC,AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
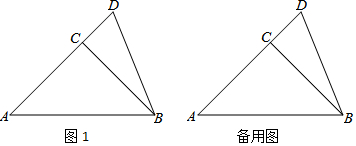
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
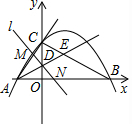 如图,已知抛物线y=ax2-2$\sqrt{3}$ax-9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
如图,已知抛物线y=ax2-2$\sqrt{3}$ax-9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com