
����Ŀ��һ����ͼ1�ij�������Ƥ���ĸ��Ƕ���ȥ�߳�Ϊ![]() �������Σ���������������һ���е��ǵ�������ͼ2�����е��泤���εij���
�������Σ���������������һ���е��ǵ�������ͼ2�����е��泤���εij���![]() ������
������![]() ��������и���������֮�ͳ�Ϊ���е�ȫ�����
��������и���������֮�ͳ�Ϊ���е�ȫ�����

��1��ͼ1��ԭ��������Ƥ�����Ϊ_![]() ������
������![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2����Ҫ�����еĸ������������ij�����ᣬÿԪǮ��Ϳ�����Ϊ![]() ����Ϳ�����������Ҫ����Ǯ������
����Ϳ�����������Ҫ����Ǯ������![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��3���Ƿ����һ�����������![]() ��ʹ�����е�ȫ����ǵ���������������������ڣ���ֱ��д�����
��ʹ�����е�ȫ����ǵ���������������������ڣ���ֱ��д�����![]() ���������ڣ���˵�����ɣ�
���������ڣ���˵�����ɣ�
���𰸡���1��12a2��420a��3600����2��Ϳ�����������Ҫ(480a��16800)Ԫ����3��a��35��7��5��1
��������
��1������ͼ�α�ʾ��ԭ��������Ƥ�ij��Ϳ���������ʾ��ԭ��������Ƥ��������ɣ�
��2������ԭ��������Ƥ�������ȥ�ĸ�С�����ε������������еı���������Ե��ۼ��ɵõ������
��3��������ڣ��г����е�ȫ����͵�����Ĺ�ʽ���������������ɣ�
�⣺��1��ԭ��Ƥ������ǣ�4a��60����3a��60����12a2��420a��3600��
�ʴ�Ϊ��12a2��420a��3600��
��2������������еı�����ǣ�12a2��2��30��4a��2��30��3a��12a2��420a��
���������������Ҫ��Ǯ���ǣ���12a2��420a����![]() ����12a2��420a����
����12a2��420a����![]() ��480a��16800��Ԫ����
��480a��16800��Ԫ����
��Ϳ�����������Ҫ(480a��16800)Ԫ��
��3�����е�ȫ�����4a��3a��4a��30��2��3a��30��2��12a2��420a��
�������4a��3a��12a2��
�������������n��ʹ12a2��420a��n��12a2
�����ã�n��1��a��35��
��a��35��n��2��a��7��n��6��a��5��n��8��a��1��n��36
���Դ������е�ȫ����ǵ������������������ʱa��35��7��5��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̨����һ����Ȼ�ֺ�������̨������ΪԲ�ģ�����Χ��ʮǧ��Χ���������籩���м�ǿ���ƻ�������ʱij̨�������ں���B�������غ�����A�����Ϸ���240ǧ�ף������ķ���Ϊ12����ÿԶ��̨������25ǧ�ף�̨��ͻ����һ������ͼ��ʾ����̨����������20ǧ��/ʱ���ٶ��ر�ƫ��30��������C�ƶ�����̨�����ĵķ������䣬���������ܷ����ﵽ��4���������̨��Ӱ�죮 ���ʣ�

��1��A�����Ƿ���ܵ�̨��Ӱ�죿��˵�����ɣ�
��2�������ܵ�̨��Ӱ�죬��ǫ̂��Ӱ��ó��еij���ʱ���ж��
��3���ó����ܵ�̨��Ӱ���������Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
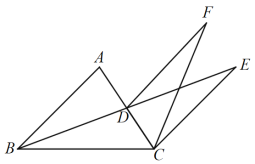
����Ŀ����ͼ�٣�����ABC�У���ABC���ACB��ƽ�����ཻ�ڵ�P��
��1�������A=80��������BPC�Ķ�����
��2����ͼ�ڣ�����ABC�����MBC����NCB�Ľ�ƽ���߽��ڵ�Q����̽����Q����A֮���������ϵ��
��3����ͼ�ۣ��ӳ��߶�BP��QC���ڵ�E����BQE�У�����һ���ڽǵ�����һ���ڽǵ�2��������A�Ķ���.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ֱ������ϵ�У���һ�ν���OAB�任����OA1B1���ڶ��ν���OA1B1�任����OA2B2�������ν���OA2B2�任����OA3B3����֪A��1��3����A1��2��3����A2��4��3����A3��8��3����B��2��0����B1��4��0����B2��8��0����B3��16��0����

��1���۲�ÿ�α任ǰ����������кα仯���ҳ����ɣ���Щ�任���ɽ���OA3B3�任����OA4B4����A4��������_______��B4��������_________��
��2�������ڣ�1����Ĺ��ɽ���OAB������n�α任���õ���OAnBn���Ƚ�ÿ�α任�������ζ��������кα仯���ҳ����ɣ����Ʋ�An��������_______��Bn��������_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=kx+b�뷴��������y= ![]() ����A����1��2����B��2��n������y�ύ��C�㣮
����A����1��2����B��2��n������y�ύ��C�㣮
��1������������һ�κ�������ʽ��
��2����ͼ1������y=kx+b����ƽ�ƣ�ʹƽ�ƺ��ֱ����y�ύ��F�㣬��˫���߽���D��E���㣬��S��ABD=3��
��D��E�����꣮
��3����ͼ2��PΪֱ��y=2�ϵ�һ�����㣬����P��PQ��y�ύֱ��AB��Q����˫������R����QR=2QP����P�����꣮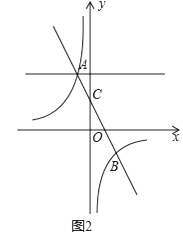
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ����������ͬһֱ����(
����������ͬһֱ����(![]() ����
����![]() ����֮��)���ס��������ֱ��
����֮��)���ס��������ֱ��![]() �С�
�С�![]() ��ͬʱ��������ֱ�߹�·������У�����������������ʻ����֪�׳����ٶȴ����ҳ����ٶȣ��ҵ��׳�����
��ͬʱ��������ֱ�߹�·������У�����������������ʻ����֪�׳����ٶȴ����ҳ����ٶȣ��ҵ��׳�����![]() ��ʱ���ס���������ֹͣ�˶����ס���������
��ʱ���ס���������ֹͣ�˶����ס���������![]() �еľ���֮��
�еľ���֮��![]() (ǧ��)��׳���ʻ��ʱ��
(ǧ��)��׳���ʻ��ʱ��![]() (Сʱ)֮��Ĺ�ϵ��ͼ��ʾ�����ҳ�����
(Сʱ)֮��Ĺ�ϵ��ͼ��ʾ�����ҳ�����![]() ��ʱ���׳���
��ʱ���׳���![]() �л���_______ǧ�ף�
�л���_______ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��
��![]() ���ϵ����ߣ�����
���ϵ����ߣ�����![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() Ϊ
Ϊ![]() ��һ�㣬����
��һ�㣬����![]() ����
����![]() ����֤��
����֤��
��1��![]() ��
��
��2��CAƽ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ͼ2��������״�ʹ�С��ȫ��ͬ�ķ���ֽ������ֽ��ÿ��С�����εı߳���Ϊ1���߶�AB�������˵����С�����εĶ����ϣ�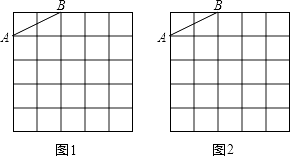
��1����ͼ1����С�����εĶ�����ȷ��һ��C������AC��BC��ʹ�á�ABCΪֱ�������Σ������Ϊ5����ֱ��д����ABC���ܳ���
��2����ͼ2����С�����εĶ�����ȷ��һ��D������AD��BD��ʹ�á�ABD����һ���ڽ�Ϊ45�㣬�����Ϊ3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֶ��������y��dm�������ȳ�x��dm����һ�κ�������������ȳ�Ϊ6dmʱ������Ϊ45.5dm����������ȳ�Ϊ14dmʱ������Ϊ105.5dm��
��1��д��y��x֮��Ĺ�ϵʽ��
��2�����ö����ȳ�10dmʱ��������Ϊ���٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com