
【题目】![]() 三个城市在同一直线上(
三个城市在同一直线上(![]() 市在
市在![]() 两市之间),甲、乙两车分别从
两市之间),甲、乙两车分别从![]() 市、
市、![]() 市同时出发沿着直线公路相向而行,两车均保持匀速行驶,已知甲车的速度大于乙车的速度,且当甲车到达
市同时出发沿着直线公路相向而行,两车均保持匀速行驶,已知甲车的速度大于乙车的速度,且当甲车到达![]() 市时,甲、乙两车都停止运动,甲、乙两车到
市时,甲、乙两车都停止运动,甲、乙两车到![]() 市的距离之和
市的距离之和![]() (千米)与甲车行驶的时间
(千米)与甲车行驶的时间![]() (小时)之间的关系如图所示,则当乙车到达
(小时)之间的关系如图所示,则当乙车到达![]() 市时,甲车离
市时,甲车离![]() 市还有_______千米.
市还有_______千米.

【答案】110
【解析】
结合图像分别表示每个特殊点的坐标,理解这些点所对应的的实际意义,根据点(0,360)可求得AB两市的距离,结合点(1.6,72)可求得两车的速度和,再结合图像中的起始点和终点可求得甲车的速度,进而求得乙车的速度,进而从甲车到达C市时到乙车到达C市时的时间,最后根据剩余路程=总路程-已行路程求得答案即可.
解:根据题意结合图像可知:点(0,360)表示A、B两市相距360千米,
点(1.6,72)表示甲乙两车行驶1.6小时时,甲车到达C市,此时乙车距离C市72千米,
则V甲+V乙=(360-72)÷1.6=180(千米/小时)
图像中的最后一个点的横坐标为3.6,表示甲乙两车行驶3.6小时时,甲车到达B市,
则V甲=360÷3.6=100(千米/小时),
∴V乙=180-100=80(千米/小时),
∴从甲车到达C市时到乙车到达C市时的时间为:72÷80=0.9(小时)
∴当乙车到达![]() 市时,甲车到
市时,甲车到![]() 市的距离为:360-100×(1.6+0.9)=110(千米)
市的距离为:360-100×(1.6+0.9)=110(千米)
故答案为:110.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿![]() 轴向右平移,当点C落在直线
轴向右平移,当点C落在直线![]() 上时,线段BC扫过的面积为( )
上时,线段BC扫过的面积为( )
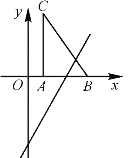
A. 16B. 8C. 8![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
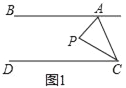
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.
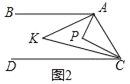
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.
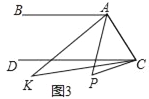
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分; B:49-45分;C:44-40分;D:39-30分;E:29-0分).每段包含最高分,不包含最低分,统计表如下,统计图如图所示.
分数段 | 频数(人) | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

根据上面提供的信息,回答下列问题:
(1)在统计表中,![]() 的值为___,
的值为___, ![]() 的值为__,并将统计图补充完整.
的值为__,并将统计图补充完整.
(2)成绩在40分以上定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张如图1的长方形铁皮,四个角都剪去边长为![]() 的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是
的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是![]() ,宽是
,宽是![]() 这个无盖铁盒各个面的面积之和称为铁盒的全面积.
这个无盖铁盒各个面的面积之和称为铁盒的全面积.

(1)图1中原长方形铁皮的面积为_![]() ;(用
;(用![]() 的代数式表示)
的代数式表示)
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可涂的面积为![]() ,则涂完这个铁盒需要多少钱?(用
,则涂完这个铁盒需要多少钱?(用![]() 的代数式表示)
的代数式表示)
(3)是否存在一个最大正整数![]() ,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个
,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
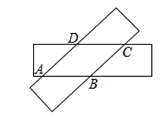
【题目】将两张宽度相等的矩形叠放在一起得到如图所示的四边形ABCD,则四边形ABCD是___________形,若两张矩形纸片的长都是10,宽都是4,那么四边形ABCD周长的最大值=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想![]() 的最小值为多少?
的最小值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,以每秒2cm的速度沿A→C→E运动,最终到达点E.若设点P运动的时间是t秒,那么当t取何值时,△APE的面积等于10?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com