
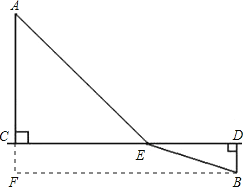
【题目】如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想![]() 的最小值为多少?
的最小值为多少?

【答案】(1)AE+BE=![]() ;(2)此时最少需要管道10km;(3)最小值为13.
;(2)此时最少需要管道10km;(3)最小值为13.
【解析】
(1)由ED=x,AC⊥CD、BD⊥CD,根据勾股定理可用x表示出AE+BE的长;(2)根据两点之间线段最短可知连接AB与CD的交点就是污水处理厂E的位置.过点B作BF⊥AC于F,构造出直角三角形,利用勾股定理求出AB的长即可;(3)根据AE+BE=![]() +
+![]() =AB=10;即可猜想所求代数式的值.
=AB=10;即可猜想所求代数式的值.
(1)在Rt△ACE和Rt△BDE中,根据勾股定理可得AE=![]() ,BE=
,BE=![]() ,
,
∴AE+BE=![]() +
+![]() ;
;
(2)根据两点之间线段最短可知连接AB与CD的交点就是污水处理厂E的位置.
过点B作BF⊥AC于F,则有BF=CD=8,BD=CF=1.
∴AF=AC+CF=6.
在Rt△ABF中,BA=![]() =
=![]() =10,
=10,
∴此时最少需要管道10km.
(3)根据以上推理,设ED=x.AC=3,DB=2,CD=12.
∴当A、E、B共线时求出AB的值即为原式最小值.
当A、E、B共线时![]() +
+![]() =
=![]() =13,即其最小值为13.
=13,即其最小值为13.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 三个城市在同一直线上(
三个城市在同一直线上(![]() 市在
市在![]() 两市之间),甲、乙两车分别从
两市之间),甲、乙两车分别从![]() 市、
市、![]() 市同时出发沿着直线公路相向而行,两车均保持匀速行驶,已知甲车的速度大于乙车的速度,且当甲车到达
市同时出发沿着直线公路相向而行,两车均保持匀速行驶,已知甲车的速度大于乙车的速度,且当甲车到达![]() 市时,甲、乙两车都停止运动,甲、乙两车到
市时,甲、乙两车都停止运动,甲、乙两车到![]() 市的距离之和
市的距离之和![]() (千米)与甲车行驶的时间
(千米)与甲车行驶的时间![]() (小时)之间的关系如图所示,则当乙车到达
(小时)之间的关系如图所示,则当乙车到达![]() 市时,甲车离
市时,甲车离![]() 市还有_______千米.
市还有_______千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.

(1)若某月用水量为18立方米,则应交水费多少元?
(2)当用水18立方米以上时,每立方米应交水费多少元?
(3)若小敏家某月交水费81元,则这个月用水量为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.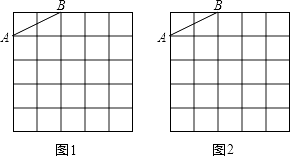
(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一根长是20 cm的细绳围成一个长方形,这个长方形的一边长为x cm,它的面积为y cm2.

(1)写出y与x之间的关系式;
(2)用表格表示当x从1变到9时(每次增加1),y的相应值;
(3)从上面的表格中,你看出什么规律?(写出一条即可)
(4)从表格中可以发现怎样围,得到的长方形的面积最大?最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB为⊙O的直径,BM为⊙O的切线,点C为射线BM上一点,连接AC交⊙O于点D,点E为BC上一点.连接AE交半圆于F.
(1)如图1,若AE平分∠BAC,求证:∠DBF=∠CBF;
(2)如图2,过点D作⊙O的切线交BM于N,若DN⊥BM,求证:△ABC为等腰直角三角形;
(3)在(2)的条件下,如图3,延长BF交AC于G,点H为AB上一点,且BH=2BE,过点H作AE的垂线交AC于P,连接OG交DN于K,若AP=CG,EF=1,求GK的长.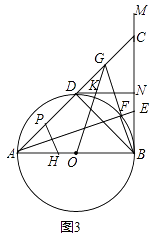
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作⊙O切线EF交BA的延长线于F.
(1)如图1,求证:EF∥AC;
(2)如图2,OP⊥AO交BE于点P,交FE的延长线于点M.求证:△PME是等腰三角形;
(3)如图3,在(2)的条件下:CG⊥AB于H点,交⊙O于G点,交AC于Q点,如图2,若sinF= ![]() ,EQ=5,求PM的值.
,EQ=5,求PM的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com