
【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作⊙O切线EF交BA的延长线于F.
(1)如图1,求证:EF∥AC;
(2)如图2,OP⊥AO交BE于点P,交FE的延长线于点M.求证:△PME是等腰三角形;
(3)如图3,在(2)的条件下:CG⊥AB于H点,交⊙O于G点,交AC于Q点,如图2,若sinF= ![]() ,EQ=5,求PM的值.
,EQ=5,求PM的值.
【答案】
(1)解:证明:连接OE,
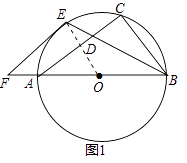
∵EF是圆的切线,
∴OE⊥FE,
∴∠F+∠FOE=90°,
∴AB为直径,
∴∠C=90°,
∴∠ABC+∠CAB=90°,
∵OE=OB,
∴∠OEB=∠OBE,
∵BE是∠B的平分线,
∴∠OBE=∠CBE,
∵∠FOE=∠OEB+∠OBE,
∴∠EOF=∠ABC,
∴∠F=∠CAB,
∴EF∥AC;
(2)解:连接OC,OE,
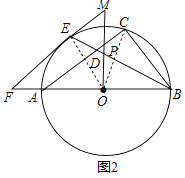
∵OP⊥AO交BE于点P,
∴∠OPB+∠OBE=90°,
∵∠OEB+∠MEB=90°,
∴∠OPB=∠MEB,
又∵∠OPB=∠EPM,
∴∠MEP=∠MPE,
∴MP=ME,
∴△PME是等腰三角形;
(3)解:连接OE,
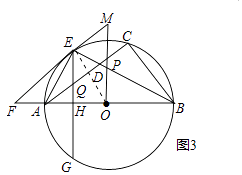
∵∠F=∠CAB,
∴sinF=sin∠CAB= ![]() ,
,
∵EG⊥AB于H点,
∴ ![]() ,
,
∴∠AEG=∠ABE,
∵∠ABE=∠EAC,
∴∠EAC=∠AEG,
∴AQ=EQ=5,
∵QH=3,AH=4,
∴EH=EQ+QH=8,
设OE=x,则OH=AO﹣AH=x﹣4,
在Rt△EHO中,x2=82+(x﹣4)2,
解得:x=10,
∴OE=10,
∵BE是∠B的平分线,
∴ ![]() ,
,
∴OE⊥AC,
∴∠CAB+∠AOD=90°,
∵∠EOM+∠AOD=90°,
∴∠EOM=∠CAB,
∴sin∠EOM= ![]() ,
,
∴tan∠EOM= ![]() =
= ![]() ,
,
∴ME= ![]() ,
,
∴PM=ME= ![]() .
.
【解析】(1)EF是圆的切线,因此;连接OE,OE⊥FE,即∠F+∠FOE=90°,AB为直径,得出∠ABC+∠CAB=90°,再证明∠OEB=∠OBE,由BE是∠B的平分线,得出∠OBE=∠CBE,再证明∠F=∠CAB,即可得出结论。
(2)连接OC,OE,由OP⊥AO得出∠OPB与∠OBE互余,∠OEB与∠MEB互余,得出∠OPB=∠MEB,再根据对顶角相等,推出MP=ME,即可得出结论。
(3)连接OE,根据已知求出sin∠CAB的值及EH的长,在Rt△EHO中,根据勾股定理建立方程,解方程求出OE的长,再证明∠EOM=∠CAB,在Rt△EPM中,求出ME的长,即可得出PM的长。
【考点精析】本题主要考查了勾股定理的概念和切线的性质定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想![]() 的最小值为多少?
的最小值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,以每秒2cm的速度沿A→C→E运动,最终到达点E.若设点P运动的时间是t秒,那么当t取何值时,△APE的面积等于10?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB、EF的端点均在小正方形的顶点上.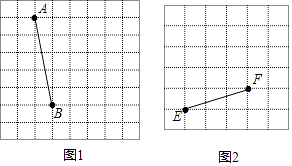
(1)如图1,作出以AB为对角线的正方形并直接写出正方形的周长;
(2)如图2,以线段EF为一边作出等腰△EFG(点G在小正方形顶点处)且顶角为钝角,并使其面积等于4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;
②△ABC的三边长分别为AB,BC,AC,若![]() +
+![]() =
=![]() ,则∠A=90°;
,则∠A=90°;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为3:4:5,则该三角形是直角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的对角线交于点E,且AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形.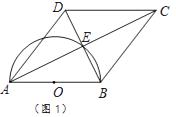
(2)如图2,若CD的延长线与半圆相切于点F,且直径AB=8.
①△ABD的面积为 .
② ![]() 的长 .
的长 . 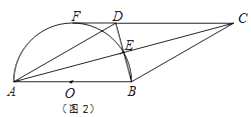
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com