
【题目】图1、图2是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB、EF的端点均在小正方形的顶点上.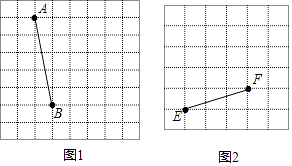
(1)如图1,作出以AB为对角线的正方形并直接写出正方形的周长;
(2)如图2,以线段EF为一边作出等腰△EFG(点G在小正方形顶点处)且顶角为钝角,并使其面积等于4.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.

(1)若某月用水量为18立方米,则应交水费多少元?
(2)当用水18立方米以上时,每立方米应交水费多少元?
(3)若小敏家某月交水费81元,则这个月用水量为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB为⊙O的直径,BM为⊙O的切线,点C为射线BM上一点,连接AC交⊙O于点D,点E为BC上一点.连接AE交半圆于F.
(1)如图1,若AE平分∠BAC,求证:∠DBF=∠CBF;
(2)如图2,过点D作⊙O的切线交BM于N,若DN⊥BM,求证:△ABC为等腰直角三角形;
(3)在(2)的条件下,如图3,延长BF交AC于G,点H为AB上一点,且BH=2BE,过点H作AE的垂线交AC于P,连接OG交DN于K,若AP=CG,EF=1,求GK的长.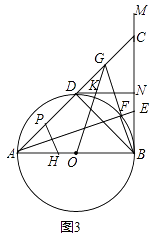
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么形如a+bi(a,b为实数)的数就叫做复数,a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3-4i)=5-3i.
(1)填空:i3=_____,i4="_______";
(2)计算:①![]() ;②
;②![]() ;
;
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:
已知:(x+y)+3i=(1-x)-yi,(x,y为实数),求x,y的值.
(4)试一试:请利用以前学习的有关知识将![]() 化简成a+bi的形式
化简成a+bi的形式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)第一版=____%,“第四版”对应扇形的圆心角为________°;
(2)请你补全条形统计图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过对角线BD上点P作直线EF,GH分别平行于AB,BC,那么图中共有( )对面积相等平行四边形.
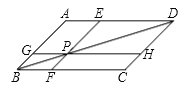
A. 1对B. 2对C. 3对D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作⊙O切线EF交BA的延长线于F.
(1)如图1,求证:EF∥AC;
(2)如图2,OP⊥AO交BE于点P,交FE的延长线于点M.求证:△PME是等腰三角形;
(3)如图3,在(2)的条件下:CG⊥AB于H点,交⊙O于G点,交AC于Q点,如图2,若sinF= ![]() ,EQ=5,求PM的值.
,EQ=5,求PM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】核桃和枣是我省著名的农特产,它们营养丰富,有益人体健康,深受老百姓喜爱。某超市从农贸批发市场批发核桃和枣进行零售,批发价和零售价格如下表所示:
名称 | 核桃 | 枣 |
批发价(元/ | 12 | 9 |
零售价(元/ | 18 | 12 |
请解答下列问题.
(1)第一天,该超市从批发市场批发核桃和枣共350![]() ,用去了3600元钱,求当天核桃和枣各批发多少kg?
,用去了3600元钱,求当天核桃和枣各批发多少kg?
(2)第二天,该超市用3600元钱仍然批发核桃和枣(批发价和零售价不变),要想将第二天批发的核桃和枣全部售完后,所获利润不低于40%,则该超市第二天至少批发核桃多少kg?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知多项式3m3n2![]() 2mn3
2mn3![]() 2中,四次项的系数为a,多项式的次数为b,常数项为c,且4b、
2中,四次项的系数为a,多项式的次数为b,常数项为c,且4b、![]() 10c3、
10c3、![]() (a+b)2bc的值分别是点A、B、C在数轴上对应的数,点P从原点O出发,沿OC方向以1单位/s的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动(点P、Q分别运动到点C、O时停止运动),两点同时出发.
(a+b)2bc的值分别是点A、B、C在数轴上对应的数,点P从原点O出发,沿OC方向以1单位/s的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动(点P、Q分别运动到点C、O时停止运动),两点同时出发.
(1)分别求4b、![]() 10c3、
10c3、![]() (a+b)2bc的值;
(a+b)2bc的值;
(2)若点Q运动速度为3单位/s,经过多长时间P、Q两点相距70;
(3)当点P运动到线段AB上时,分别取OP和AB的中点E、F,试问![]() 的值是否变化,若变化,求出其范围:若不变,求出其值.
的值是否变化,若变化,求出其范围:若不变,求出其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com