
【题目】如图,在矩形![]() 中,
中,![]() 于
于![]()
![]() 且
且![]() 则
则![]() 的长度是( )
的长度是( )

A. 3B. 5C. ![]() D.
D. ![]()
【答案】D
【解析】
根据∠EDC:∠EDA=1:3,可得∠EDC=22.5°,∠EDA=67.5°,再由AC=10,求得DE.
∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=10,OA=OC=![]() AC=5,OB=OD=
AC=5,OB=OD=![]() BD=5,
BD=5,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,
∴∠EDC=22.5°,∠EDA=67.5°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DCE=90°-∠EDC=67.5°,
∴∠ODC=∠OCD=67.5°,
∴∠ODC+∠OCD+∠DOC=180°,
∴∠COD=45°,
∴OE=DE,
∵OE2+DE2=OD2,
∴2DE2=OD2=25,
∴DE=![]() ,
,
故选D.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;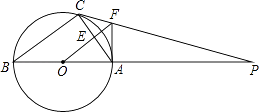
(1)判断AF与⊙O的位置关系并说明理由.
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校男子足球队的年龄分布如条形图所示,则这些队员年龄的众数、中位数、平均数分别是( )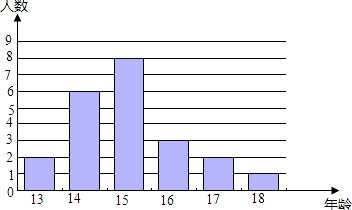
A.15、14、15
B.14、15、15
C.15、15、14
D.15、15、15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小明家和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的是哪些地方?
(2)学校、商场和停车场分别在小明家的什么方位?
(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 三个城市在同一直线上(
三个城市在同一直线上(![]() 市在
市在![]() 两市之间),甲、乙两车分别从
两市之间),甲、乙两车分别从![]() 市、
市、![]() 市同时出发沿着直线公路相向而行,两车均保持匀速行驶,已知甲车的速度大于乙车的速度,且当甲车到达
市同时出发沿着直线公路相向而行,两车均保持匀速行驶,已知甲车的速度大于乙车的速度,且当甲车到达![]() 市时,甲、乙两车都停止运动,甲、乙两车到
市时,甲、乙两车都停止运动,甲、乙两车到![]() 市的距离之和
市的距离之和![]() (千米)与甲车行驶的时间
(千米)与甲车行驶的时间![]() (小时)之间的关系如图所示,则当乙车到达
(小时)之间的关系如图所示,则当乙车到达![]() 市时,甲车离
市时,甲车离![]() 市还有_______千米.
市还有_______千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 且
且![]() 点在线段
点在线段![]() 上,连接
上,连接![]() .
.
(1)如图1,若![]() 求线段
求线段![]() 的长;
的长;

(2)如图1,若![]() 求证:
求证:![]()
(3)如图2,在第(2)问的条件下,若点![]() 在
在![]() 的延长线上时,连接
的延长线上时,连接![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 的面积为
的面积为![]() .直接写出
.直接写出![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.

(1)若某月用水量为18立方米,则应交水费多少元?
(2)当用水18立方米以上时,每立方米应交水费多少元?
(3)若小敏家某月交水费81元,则这个月用水量为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一根长是20 cm的细绳围成一个长方形,这个长方形的一边长为x cm,它的面积为y cm2.

(1)写出y与x之间的关系式;
(2)用表格表示当x从1变到9时(每次增加1),y的相应值;
(3)从上面的表格中,你看出什么规律?(写出一条即可)
(4)从表格中可以发现怎样围,得到的长方形的面积最大?最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么形如a+bi(a,b为实数)的数就叫做复数,a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3-4i)=5-3i.
(1)填空:i3=_____,i4="_______";
(2)计算:①![]() ;②
;②![]() ;
;
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:
已知:(x+y)+3i=(1-x)-yi,(x,y为实数),求x,y的值.
(4)试一试:请利用以前学习的有关知识将![]() 化简成a+bi的形式
化简成a+bi的形式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com