
【题目】如图,![]() 且
且![]() 点在线段
点在线段![]() 上,连接
上,连接![]() .
.
(1)如图1,若![]() 求线段
求线段![]() 的长;
的长;

(2)如图1,若![]() 求证:
求证:![]()
(3)如图2,在第(2)问的条件下,若点![]() 在
在![]() 的延长线上时,连接
的延长线上时,连接![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 的面积为
的面积为![]() .直接写出
.直接写出![]() 之间的数量关系.
之间的数量关系.

【答案】(1)线段AB的长为6;(2)见解析;(3)c+a=2b.
【解析】
(1)通过“SAS”可证△ACD≌△BCE,由此可得BE=AD=4,结合AE=2即可得解;
(2)在AD上取一点H,使得AH=AE,先证△ACH≌△ACE,可得CH=CE,进而可证CH=CD,利用三线合一可得DH=2DF,最后根据AD=DH+AH等量代换即可得证;
(3)过点C作CG⊥AB于点G,同理可证△ACD≌△BCE,进而得BE=AD,∠CAD=∠B=45°,∠D=∠CEB,证得CF∥AB便可证得S△AEC=S△AEF=a,再证△CFD≌△CGE可得S△CGE=S△CFD=b,
根据三线合一可得AG=BG便可得S△BCG=S△BCG,进而得解.
(1)证明:∵∠ACB=∠DCE=90°,
∴∠ACE+∠ECB=∠ACE+∠DCA,
∴∠ECB=∠DCA,
在△ACD与△BCE中,

∴△ACD≌△BCE(SAS),
∴BE=AD,
∵AD=4,
∴BE=4,
又∵AE=2,
∴AB=AE+BE=6,
∴线段AB的长为6;
(2)证明:如图,在AD上取一点H,使得AH=AE,连接CH,

∵AC=BC,∠ACB=90°,
∴∠B=∠CAB=45°,
∵△ACD≌△BCE,
∴∠CAD=∠B=45°,BE=AD,
在△ACH与△ACE中,

∴△ACH≌△ACE(SAS),
∴CH=CE,
∵CD=CE,
∴CH=CD,
又∵CF⊥AD,
∴DF=FH,
∴DH=2DF,
∵AD=DH+AH,
∴BE=2DF+AE;
(3)解:如图,过点C作CG⊥AB于点G,

∵∠ACB=∠DCE=90°,
∴∠ACE+∠ACB=∠ACE+∠DCE,
∴∠ECB=∠DCA,
在△ACD与△BCE中,

∴△ACD≌△BCE(SAS),
∴BE=AD,∠CAD=∠B=45°,∠D=∠CEB,
∴∠BAD=∠CAD+∠CAB=90°,
又∵CF⊥AD,
∴CF∥AB,
∴S△AEC=S△AEF=a,
∵△ACD≌△BCE,
∴S△ACD=S△BCE,
∴CF⊥AD,CG⊥AB,
∴∠CFD=∠CGE=90°,
在△CFD与△CGE中,
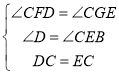
∴△CFD≌△CGE(AAS),
∴S△CGE=S△CFD=b,
∴S△CGA=S△CGE-S△AEC=b-a,
∵S△BCE=c,
∴S△BCG=S△BCE-S△CGE=c-b,
∵AC=BC,CG⊥AB,
∴AG=BG,
∴S△BCG=S△BCG,
∴c-b=b-a,
即:c+a=2b.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数![]() 的图象交于点A(-1,2),B(m,-1).
的图象交于点A(-1,2),B(m,-1).
(1)求一次函数与反比例函数的解析式;
(2)在x轴上是否存在点P(n,0),使△ABP为等腰三角形,请你直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为 . 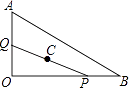
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲,乙两军区进行军事演练,乙军区在河东岸![]() 处,因不知河宽,甲军的狙击手在
处,因不知河宽,甲军的狙击手在![]() 处很难瞄准乙军军营,于是甲军连长站在西岸的点
处很难瞄准乙军军营,于是甲军连长站在西岸的点![]() 处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到乙军军营
处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到乙军军营![]() 处,然后他后退到
处,然后他后退到![]() 点,这时他的视点恰好落在
点,这时他的视点恰好落在![]() 处,此时他只需测量脚站的
处,此时他只需测量脚站的![]() 点和
点和![]() 点的距高,即可知道狙击手与乙军军营的距离,他判断的依据是( )
点的距高,即可知道狙击手与乙军军营的距离,他判断的依据是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )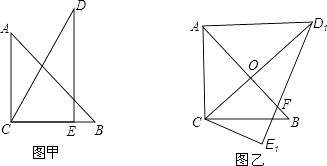
A.![]()
B.5
C.4
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
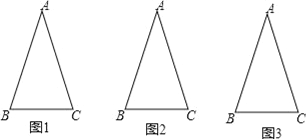
【题目】如图,△ABC中,AB=AC,∠A=36°,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括△ABC)
(1)在图1中画1条线段,使图中有2个等腰三角形,并直接写出这2个等腰三角形的顶角度数分别是 度和 度;
(2)在图2中画2条线段,使图中有4个等腰三角形;
(3)继续按以上操作发现:在△ABC中画n条线段,则图中有 个等腰三角形,其中有 个黄金等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 . 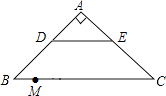
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com