
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 . 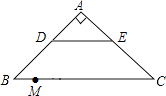
【答案】![]() 或
或 ![]()
【解析】解:如图作EF⊥BC于F,DN′⊥BC于N′交EM于点O′,此时∠MN′O′=90°,
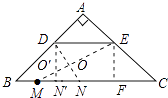
∵DE是△ABC中位线,
∴DE∥BC,DE= ![]() BC=10,
BC=10,
∵DN′∥EF,
∴四边形DEFN′是平行四边形,∵∠EFN′=90°,
∴四边形DEFN′是矩形,
∴EF=DN′,DE=FN′=10,
∵AB=AC,∠A=90°,
∴∠B=∠C=45°,
∴BN′=DN′=EF=FC=5,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DO′= ![]() .
.
当∠MON=90°时,
∵△DOE∽△EFM,
∴ ![]() =
= ![]() ,
,
∵EM= ![]() =13,
=13,
∴DO= ![]() ,
,
故答案为 ![]() 或
或 ![]() .
.
此题分两种情况讨论:作EF⊥BC于F,DN′⊥BC于N′交EM于点O′,当∠MN′O′=90°,根据平行得线段成比例,建立方程,求解即可。;当∠MON=90°时,△DOE∽△EFM,得对应边成比例,建立方程求解即可。


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 且
且![]() 点在线段
点在线段![]() 上,连接
上,连接![]() .
.
(1)如图1,若![]() 求线段
求线段![]() 的长;
的长;

(2)如图1,若![]() 求证:
求证:![]()
(3)如图2,在第(2)问的条件下,若点![]() 在
在![]() 的延长线上时,连接
的延长线上时,连接![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 的面积为
的面积为![]() .直接写出
.直接写出![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )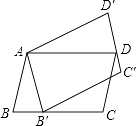
A.100°
B.105°
C.115°
D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么形如a+bi(a,b为实数)的数就叫做复数,a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3-4i)=5-3i.
(1)填空:i3=_____,i4="_______";
(2)计算:①![]() ;②
;②![]() ;
;
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:
已知:(x+y)+3i=(1-x)-yi,(x,y为实数),求x,y的值.
(4)试一试:请利用以前学习的有关知识将![]() 化简成a+bi的形式
化简成a+bi的形式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过对角线BD上点P作直线EF,GH分别平行于AB,BC,那么图中共有( )对面积相等平行四边形.
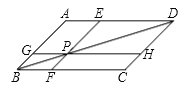
A. 1对B. 2对C. 3对D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
图1

图2

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com