
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;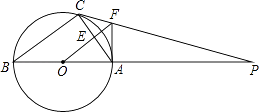
(1)判断AF与⊙O的位置关系并说明理由.
(2)若⊙O的半径为4,AF=3,求AC的长.
【答案】
(1)解:证明:连接OC,如图所示:

∵AB是⊙O直径,
∴∠BCA=90°,
∵OF∥BC,
∴∠AEO=90°,∠1=∠2,∠B=∠3,
∴OF⊥AC,
∵OC=OA,
∴∠B=∠1,
∴∠3=∠2,
在△OAF和△OCF中,
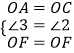 ,
,
∴△OAF≌△OCF(SAS),
∴∠OAF=∠OCF,
∵PC是⊙O的切线,
∴∠OCF=90°,
∴∠OAF=90°,
∴FA⊥OA,
∴AF是⊙O的切线;
(2)解:∵⊙O的半径为4,AF=3,∠OAF=90°,
∴OF= ![]() =
= ![]() =5
=5
∵FA⊥OA,OF⊥AC,
∴AC=2AE,△OAF的面积= ![]() AFOA=
AFOA= ![]() OFAE,
OFAE,
∴3×4=5×AE,
解得:AE= ![]() ,
,
∴AC=2AE= ![]() .
.
【解析】(1)要证切线可证垂直,由CF是切线须连接OC,得垂直,证出△OAF≌△OCF,得到∠OAF=∠OCF,由切线得∠OCF=90°,进而∠OAF=90度,证出切线;(2)由面积法先求出AE,进一步求出AC.


科目:初中数学 来源: 题型:
【题目】已知∠MON = 50°,OE 平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D、设∠OAC = x°.
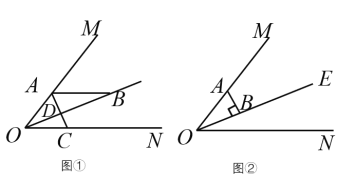
(1)如图①,若AB//ON,
①则∠ABO 的度数是________;
②当∠BAD =∠ABD 时,x=_______;当∠BAD = ∠BDA 时,x=________.
(2)如图②,若AB⊥OE,则是否存在这样的x值,使得 △ABD 中有一个角是另一个角的两倍.存在,直接写出x的值;不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年某企业按餐厨垃圾处理费50元/吨、建筑垃圾处理费20元/吨的收费标准,共支付餐厨和建筑垃圾处理费7000元.从2016年元月起,收费标准上调为:餐厨垃圾处理费120元/吨,建筑垃圾处理费40元/吨.若该企业2016年处理的这两种垃圾数量与2015年相比没有变化,就要多支付垃圾处理费8600元.
(1)该企业2015年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2016年将上述两种垃圾处理总量减少到200吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2016年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
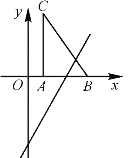
【题目】如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿![]() 轴向右平移,当点C落在直线
轴向右平移,当点C落在直线![]() 上时,线段BC扫过的面积为( )
上时,线段BC扫过的面积为( )
A. 16B. 8C. 8![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数![]() 的图象交于点A(-1,2),B(m,-1).
的图象交于点A(-1,2),B(m,-1).
(1)求一次函数与反比例函数的解析式;
(2)在x轴上是否存在点P(n,0),使△ABP为等腰三角形,请你直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】收集和整理数据.
某中学七(1)班学习了统计知识后,数学老师要求每个学生就本班学生的上学方式进行一次全面调查,如图是一同学通过收集数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题:(每个学生只选择1种上学方式).

(1)求该班乘车上学的人数;
(2)将频数分布直方图补充完整;
(3)若该校七年级有1200名学生,能否由此估计出该校七年级学生骑自行车上学的人数,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com