
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题。

(1)在第4个图中,共有白色瓷砖 块;在第![]() 个图中,共有白色瓷砖 块;
个图中,共有白色瓷砖 块;
(2)在第4个图中,共有瓷砖 块;在第![]() 个图中,共有瓷砖 块;
个图中,共有瓷砖 块;
(3)如果每块黑瓷砖4元,白瓷砖3元,铺设当![]() 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖?
【答案】(1)20,n2+n;(2)42,(n+2)(n+3);(3)514元
【解析】
试题分析:(1)通过观察发现规律,然后将n=4代入即可;
(2)将黑色瓷砖和白色瓷砖加在一起即可得到答案;
(3)求出当n=10时黑色和白色瓷砖的个数,然后计算总费用即可.
(1)通过观察图形可知,当n=1时,用白瓷砖2块,黑瓷砖10块;
当n=2时,用白瓷砖6块,黑瓷砖14块;
当n=3时,用白瓷砖12块,黑瓷砖18块;
可以发现,需要白瓷砖的数量和图形数之间存在这样的关系,即白瓷砖块数等于图形数的平方加上图形数;
需要黑瓷砖的数量和图形数之间存在这样的关系,即黑瓷砖块数等于图形数的4倍加上图形数.
所以,在第n个图形中,白瓷砖的块数可用含n的代数式表示为![]() ;
;
黑瓷砖的块数可用含n的代数式表示为4n+6.
∴当n=4时,白色瓷砖有![]() 块;
块;
(2)由(1)可得总块数可表示为![]() ;
;
(3)观察图形可知,每-横行有白砖(n+1)块,每-竖列有白砖n块,
因而白砖总数是n(n+1)块,n=10时,白砖为10×11=110(块),黑砖数为46(块).
故总钱数为110×3+46×4=330+184=514(元),
答:共花514元钱购买瓷砖.


科目:初中数学 来源: 题型:
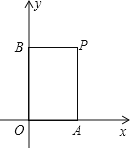
【题目】在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点。例如,图中过点p分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点p是和谐点。
判断点M(1,2),N(4,4)是否为和谐点,并说明理由;
若和谐点P(a,3)在直线y=-x+b(b为常数)上,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
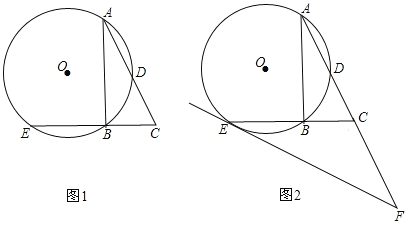
【题目】(2016四川省乐山市第25题)已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O于点E.
(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;
(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.
①若CF=CD时,求sin∠CAB的值;
②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑3 000元,购买1台学习机800元.
(1)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168 000元,则购买平板电脑最多多少台?
(2)在(1)的条件下,购买学习机的台数不超过平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
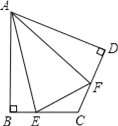
【题目】(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD;
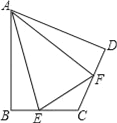
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立?
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com