
 如图,在△ABC中,AC=BC,D是AC上一点,DE∥AB交BC于点E,且AD=DE,F是AB上一点,BF=BE,连接FD.
如图,在△ABC中,AC=BC,D是AC上一点,DE∥AB交BC于点E,且AD=DE,F是AB上一点,BF=BE,连接FD.分析 (1)结论:四边形ADEB是等腰梯形.首先证明四边形ADEB是梯形,再证明∠A=∠B即可;
(2)只要证明四边形BEDF是平行四边形即可;
解答 解:(1)结论:四边形ADEB是等腰梯形.
理由:∵AC、BC是△ABC的两边,
∴AC与BC不平行,即BE与AD不平行,
∵DE∥AB,
∴四边形ADEB是梯形,
∵AC=BC,
∴∠A=∠B,
∴梯形ADEB是等腰梯形.
(2)∵梯形ADEB是等腰梯形,
∴AD=BE,
∵AD=ED,
∴BE=DE,
∵BE=BF,
∴DE=BF,
∵DE∥AB,
∴四边形BEDF是平行四边形,
∴BE=FD.
点评 本题考查平行四边形的性质、等腰梯形的判定和性质、等腰三角形的性质等知识,解题的关键是掌握等腰梯形的判定方法,平行四边形的判定方法,属于中考常考题型.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:选择题
| A. | a=-3,b=2 | B. | a=3,b=2 | C. | a=-3,b=-2 | D. | a=3,b=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>b,则2a>2b | B. | 若-2a<-2b,则a>b | ||
| C. | 若a-1<b-1,则a>b | D. | 若a>b,则-a-1<-b-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:| 组别 | 成绩x(分) | 频数(人数) | 频率 |
| 一 | 50≤x<60 | 2 | 0.04 |
| 二 | 60≤x<70 | 10 | 0.2 |
| 三 | 70≤x<80 | 14 | b |
| 四 | 80≤x<90 | a | 0.32 |
| 五 | 90≤x<100 | 8 | 0.16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2014 | D. | 2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
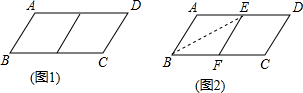
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com