
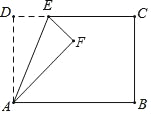
ЎѕМвДїЎїИзНјЈ¬ФЪ±Яі¤ОЄ4µДХэ·ЅРОABCDЦРЈ¬PКЗBC±ЯЙПТ»¶ЇµгЈЁІ»УлBЎўCБЅµгЦШєПЈ©Ј¬Ѕ«ЎчABPСШЦ±ПЯAP·ХЫЈ¬µгBВдФЪµгEґ¦Ј»ФЪCDЙПИЎТ»µгMЈ¬К№µГЅ«ЎчCMPСШЦ±ПЯMP·Хۺ󣬵гCВдФЪЦ±ПЯPEЙПµДµгFґ¦Ј¬Ц±ПЯPEЅ»CDУЪµгNЈ¬Б¬ЅУAMЎўANЈ®

ЈЁ1Ј©ИфPОЄBCµДЦРµгЈ¬ФтsinЎПCPM=________Ј»
ЈЁ2Ј©ЗуЦ¤ЈєЎПPANµД¶ИКэІ»±дЈ»
ЈЁ3Ј©µ±PФЪBC±ЯЙПФЛ¶ЇК±Ј¬ЎчADMµДГж»эКЗ·сґжФЪЧоРЎЦµЈ¬ИфґжФЪЈ¬ЗлЗуіцPBµДі¤Ј»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©Ц¤ГчјыЅвОцЈ»ЈЁ3Ј©ґжФЪЧоРЎЦµЈ¬BPЈЅ2.
Ј»ЈЁ2Ј©Ц¤ГчјыЅвОцЈ»ЈЁ3Ј©ґжФЪЧоРЎЦµЈ¬BPЈЅ2.
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁ1Ј©ёщѕЭХэ·ЅРОµДРФЦКєН№ґ№Й¶ЁАнЗуіцAPЈ¬ёщѕЭХэПТµД¶ЁТеµГµЅsinЎПBAPЈЅ![]() Ј¬ёщѕЭХЫµюµДРФЦКЦ¤ГчЎПCPMЈЅЎПBAPЈ¬µГµЅґр°ёЈ»
Ј¬ёщѕЭХЫµюµДРФЦКЦ¤ГчЎПCPMЈЅЎПBAPЈ¬µГµЅґр°ёЈ»
ЈЁ2Ј©Ц¤ГчRtЎчAENЎХRtЎчADNЈ¬µГµЅЎПEANЈЅЎПDANЈ¬јЖЛгјґїЙЈ»
ЈЁ3Ј©ЙиPBЈЅxЈ¬ёщѕЭПаЛЖИэЅЗРОµДРФЦКЗуіцDMЈ¬ёщѕЭИэЅЗРОµДГж»э№«КЅµГµЅ¶юґОєЇКэµДЅвОцКЅЈ¬И»єуЅ«ЅвОцКЅЧЄ»ЇОЄ¶ҐµгКЅЈ¬јґїЙµГіцґр°ёЈ®
КФМвЅвОцЈє
ЅвЈєЈЁ1Ј©ЎЯХэ·ЅРОABCDµД±Яі¤ОЄ4Ј¬PОЄBCµДЦРµгЈ¬
ЎаBPЈЅ![]() PCЈЅ2Ј¬
PCЈЅ2Ј¬
ЎаAPЈЅ![]() ЈЅ2
ЈЅ2![]() Ј¬
Ј¬
ЎаsinЎПBAPЈЅ![]() Ј¬
Ј¬
УЙХЫµюµДРФЦКїЙЦЄЈ¬ЎПBPAЈЅЎПEPAЈ¬ЎПCPMЈЅЎПFPMЈ¬
ЎаЎПAPMЈЅ![]() ЈЁЎПBPEЈ«ЎПCPFЈ©ЈЅ90ЎгЈ¬
ЈЁЎПBPEЈ«ЎПCPFЈ©ЈЅ90ЎгЈ¬
ЎаЎПBPAЈ«ЎПCPMЈЅ90ЎгЈ¬УЦЎПBPAЈ«ЎПBAPЈЅ90ЎгЈ¬
ЎаЎПCPMЈЅЎПBAPЈ¬
ЎаsinЎПCPMЈЅsinЎПBAPЈЅ![]() Ј¬
Ј¬
№Кґр°ёОЄЈє ![]() Ј»
Ј»
ЈЁ2Ј©ЅвЈєУЙХЫµюµДРФЦКїЙЦЄЈ¬ЎПAEPЈЅЎПBЈЅ90ЎгЈ¬AEЈЅABЈ¬ЎПBAPЈЅЎПEAPЈ¬
ЎаAEЈЅADЈ¬
ФЪRtЎчAENєНRtЎчADNЦРЈ¬
AEЈЅADЈ¬ANЈЅANЈ¬
ЎаRtЎчAENЎХRtЎчADNЈ¬
ЎаЎПEANЈЅЎПDANЈ¬
ЎаЎПPANЈЅ![]() ЎПBADЈЅ45ЎгЈ»
ЎПBADЈЅ45ЎгЈ»
ЈЁ3Ј©ЅвЈєЙиPBЈЅxЈ¬ФтPCЈЅ4©ЃxЈ¬
ЎЯЎПCPMЈЅЎПBAPЈ¬ЎПABPЈЅЎПPCMЈЅ90ЎгЈ¬
ЎаЎчABPЎЧЎчPCMЈ¬
Ўа![]() Ј¬јґ
Ј¬јґ![]() Ј¬
Ј¬
ЅвµГЈ¬CMЈЅ©Ѓ![]() x2Ј«xЈ¬
x2Ј«xЈ¬
ЎаDMЈЅ4©ЃЈЁ©Ѓ![]() x2Ј«xЈ©ЈЅ
x2Ј«xЈ©ЈЅ ![]() x2©ЃxЈ«4Ј¬
x2©ЃxЈ«4Ј¬
ЎаЎчADMµДГж»эЈЅ![]() ЎБ4ЎБЈЁ
ЎБ4ЎБЈЁ![]() x2©ЃxЈ«4Ј©ЈЅ
x2©ЃxЈ«4Ј©ЈЅ![]() ЈЁx©Ѓ2Ј©2Ј«6Ј¬
ЈЁx©Ѓ2Ј©2Ј«6Ј¬
Ўаµ±BPЈЅ2К±Ј¬ЎчADMµДГж»эґжФЪЧоРЎЦµ6Ј®


 є®јЩС§УлБ·ПµБРґр°ё
є®јЩС§УлБ·ПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪѕШРОABCDЦРЈ¬AD=5Ј¬AB=8Ј¬µгEОЄЙдПЯDCЙПТ»ёц¶ЇµгЈ¬°СЎчADEСШЦ±ПЯAEХЫµюЈ¬µ±µгDµД¶ФУ¦µгFёХєГВдФЪПЯ¶ОABµДґ№Ц±ЖЅ·ЦПЯЙПК±Ј¬ФтDEµДі¤ОЄ_____Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї№ШУЪЖµВКУлёЕВКУРПВБРјёЦЦЛµ·ЁЈ¬ЖдЦРХэИ·µДЛµ·ЁКЗЈЁ Ј©
ўЩЎ°ГчМмПВУкµДёЕВККЗ90%Ў±±нКѕГчМмПВУкµДїЙДЬРФєЬґуЈ»
ўЪЎ°ЕЧТ»Г¶УІ±ТХэГжіЇЙПµДёЕВКОЄ![]() Ў±±нКѕГїЕЧБЅґОѕНУРТ»ґОХэГжіЇЙПЈ»
Ў±±нКѕГїЕЧБЅґОѕНУРТ»ґОХэГжіЇЙПЈ»
ўЫЎ°ЕЧТ»Г¶УІ±ТХэГжіЇЙПµДёЕВКОЄ![]() Ў±±нКѕЛжЧЕЕЧЦАґОКэµДФцјУЈ¬Ў°ЕЧіцХэГжіЇЙПЎ±ХвТ»КВјю·ўЙъµДЖµВКОИ¶ЁФЪ
Ў±±нКѕЛжЧЕЕЧЦАґОКэµДФцјУЈ¬Ў°ЕЧіцХэГжіЇЙПЎ±ХвТ»КВјю·ўЙъµДЖµВКОИ¶ЁФЪ![]() ёЅЅьЈ»
ёЅЅьЈ»
ўЬЎ°ДіІКЖ±ЦРЅ±µДёЕВККЗ1%Ў±±нКѕВт100ХЕёГЦЦІКЖ±І»їЙДЬЦРЅ±.
A.ўЩўЫB.ўЩўЬC.ўЪўЫD.ўЪўЬ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїРЗЖЪМмЈ¬БбБбЖпЧФРРіµµЅЅјНвУОНжЈ¬ЛэАлјТµДѕаАлУлК±јдµД№ШПµИзНјЛщКѕЈ¬ЗлёщѕЭНјПу»ШґрПВБРОКМвЈ®

ЈЁ1Ј©БбБбµЅґпАлјТЧоФ¶µДµШ·ЅКЗКІГґК±јдЈїАлјТ¶аФ¶Јї
ЈЁ2Ј©ЛэєОК±їЄКјµЪТ»ґОРЭПўЈїРЭПўБЛ¶аі¤К±јдЈї
ЈЁ3Ј©ЛэЖпіµЛЩ¶ИЧоїмКЗФЪКІГґК±єтЈїіµЛЩ¶аЙЩЈї
ЈЁ4Ј©БбБбИ«іМЖпіµµДЖЅѕщЛЩ¶ИКЗ¶аЙЩЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј,ФЪБвРОABCDЦР,AB=6,ЎПDAB=60Ўг,AE·Ц±рЅ»BCЎўBDУЪµгEЎўF,ИфCE=2,Б¬ЅУCF.ТФПВЅбВЫ:ўЩЎПBAF=ЎПBCF; ўЪµгEµЅABµДѕаАлКЗ2![]() ; ўЫSЎчCDFЈєSЎчBEF=9Јє4; ўЬtanЎПDCF=3/7. ЖдЦРХэИ·µДУР()
; ўЫSЎчCDFЈєSЎчBEF=9Јє4; ўЬtanЎПDCF=3/7. ЖдЦРХэИ·µДУР()

A. 4ёц B. 3ёц C. 2ёц D. 1ёц
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪН¬Т»Чш±кПµЦРЈ¬Т»ґОєЇКэy=©Ѓmx+n2Ул¶юґОєЇКэy=x2+mµДНјПуїЙДЬКЗЈЁЎЎЎЎЈ©
A.  B.
B.  C.
C.  D.
D. 
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїјЧТТБЅИЛНжГюЗтУОП·ЈєТ»ёцІ»НёГчµДґьЧУЦРЧ°УРПаН¬ґуРЎµД3ёцЗтЈ¬ЗтЙП·Ц±р±кУРКэЧЦ1Ј¬2Ј¬3Ј®КЧПИЈ¬јЧґУЦРЛж»ъГюіцТ»ёцЗтЈ¬И»єуЈ¬ТТґУКЈПВµДЗтЦРЛж»ъГюіцТ»ёцЗтЈ¬±ИЅПЗтЙПµДКэЧЦЈ¬ЅПґуµД»сК¤Ј®
ЈЁ1Ј©ЗујЧГюµЅ±кУРКэЧЦ3µДЗтµДёЕВКЈ»
ЈЁ2Ј©ХвёцУОП·№«ЖЅВрЈїЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЕЧОпПЯy=ax2+bx©Ѓ4УлxЦбЅ»УЪAЈЁ4Ј¬0Ј©ЎўBЈЁ©Ѓ2Ј¬0Ј©БЅµгЈ¬УлyЦбЅ»УЪµгCЈ¬µгPКЗПЯ¶ОABЙПТ»¶ЇµгЈЁ¶ЛµгіэНвЈ©Ј¬№эµгPЧчPDЎОACЈ¬Ѕ»BCУЪµгDЈ¬Б¬ЅУCPЈ®

ЈЁ1Ј©ЗуёГЕЧОпПЯµДЅвОцКЅЈ»
ЈЁ2Ј©µ±¶ЇµгPФЛ¶ЇµЅєОґ¦К±Ј¬BP2=BDBCЈ»
ЈЁ3Ј©µ±ЎчPCDµДГж»эЧоґуК±Ј¬ЗуµгPµДЧш±кЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЛД±ЯРОABCDЦРЈ¬ЎПABC=90ЎгЈ¬AC=ADЈ¬MЈ¬N·Ц±рОЄACЈ¬ADµДЦРµгЈ¬
ЗТЎПABM=ЎПBAMЈ¬Б¬ЅУBMЈ¬MNЈ¬BNЈ®
ЈЁ1Ј©ЗуЦ¤ЈєBM=MNЈ»
ЈЁ2Ј©ЎПBAD=60ЎгЈ¬ACЖЅ·ЦЎПBADЈ¬AC=2Ј¬ЗуBNµДі¤Ј®

Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com